Файл: 9. Введите понятие производной второго, третьего и т д.docx

Введите понятие монотонной функции. Сформулируйте и докажите признак монотонности функции, объясните его геометрический смысл. Проиллюстрируйте его применение на конкретном примере.

Функция называется монотонной на промежутке, если она на этом промежутке или возрастает, или убывает. Функция называется монотонной на какой-то области, если ее приращение не меняет знак и остается постоянным (по знаку) всегда на этой области.

Признак монотонности. Пусть функция f(x): непрерывна на некотором промежутке x с концами a и b; дифференцируема во всех внутренних точках (a, b) тогда для того чтобы y=f(x) возрастала(убывала) ⇔чтобы f ’(x) ≥0 (неотрицательна) (f ’(x) 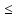0 (неположительна)) во всех внутренних точках промежутка x на (a,b). Если во всех внутренних точках x f ’(x)>0(f ’(x)<0), то f(x)- строго возрастает(убывает).

Доказательство:

1. Необходимость. Пусть f(x) возрастает(убывает) на х с концами (a,b). По определению, если х1< х2, то f(х₁)< f(х₂). Пусть х₀∈Х, возьмем ∆х такое, что ∆х>0 и U(x₀+∆х) ∈Х ⇒ x₀+∆х>х⇒ т.к. f(x)-возрастает(убывает), то f(x₀+∆х)-f(x₀)>0 (f(x₀+∆х)-f(x₀)<0).

Рассмотрим отношение ( ).

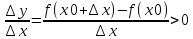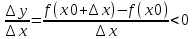Переходя к пределу имеем 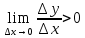⇒f ’(x)>0( 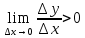⇒f ’(x)<0) чтд.

2. Достаточность. Пусть х₁< х₂ , х₁ и х₂∈Х, тогда по формуле Лагранжа имеем: f(x₂)- f(x₁)=f ’( 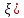( х₂ -х₁). Нам дано f ’(x) ≥0 ⇒ f ’( 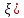≥0 ⇒ f(x₂)- f(x₁) ≥0 ⇒ f(x₂) ≥f(x₁) ⇒ f(x)-возрастает на Х.(аналогично f ’(x) 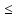0)

Если f ’(x) 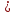0 ⇒ f ’( 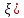>0 ⇒ f(x₂)- f(x₁) >0 ⇒ f(x₂) >f(x₁) ⇒ f(x)-строго возрастает на Х. (аналогично f ’(x)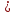

---

0)

f (x) –возрастает (угол острый)

f (x) –убывает (угол тупой)

9. Введите понятие точек экстремума (максимума и минимума) и экстремума функции. Сформулируйте необходимое условие экстремума и проиллюстрируйте его геометрически. Сформулируйте и докажите достаточное условие экстремума функции в терминах первой производной.

Пусть функция определена в некоторой окрестности точки х_0. Тогда х₀ называется точкой максимума(минимума) функции если существует δ окрестность точки х₀(х₀-δ, х₀+δ), такая, что для любого x∈(х₀-δ, х₀+δ) выполняется неравенство f ’(x) f(x₀) (соответственно f ’(x) ≥f(x₀)).

Точки минимума и максимума называются точками экстремума.

Необходимое условие экстремума. Пусть х₀ является точкой экстремума функции f, определенной в некоторой окрестности точки х₀. Тогда либо производная f ’(x) не существует, либо равна 0.

Достаточное условие экстремума. Пусть точка х₀ является точкой возможного экстремума(критической). f(x) дифференцируема всюду в некоторой окрестности точки х₀. Тогда если в этой окрестности слева от точки х₀ выполняется неравенство f ’(x)>0 а справа f ’(x)<0, то в точке х₀ функция имеет максиму, а если при х₀-δ< х<x₀ выполняется неравенство f ’(x)<0, а при х₀ < х<x₀+δ неравенство f ’(x)>0, то х точка минимума.

Доказательство(для максимума):

1. 
   Пусть f ’(x)>0 при x∈(х₀-δ, х₀) и f ’(x)<0 при x∈(х₀, х₀+δ). Надо доказать, что f ’(x)-наибольшее значение в окрестности x_0. Достаточно доказать, что f(x₀)-f(x)>0 при любых х∈(х₀-δ, х₀+δ). Функция дифференцируема в U(х₀,δ) ⇒непрерывна в U(х₀,δ) и в частности на [x₀,x]. f(x₀)-f(x)= f ’( ( х₀ -х) ⇒ f(x₀)-f(x)>0, т.е. f(x₀) >f(x), т.е. f(x₀)- наибольшее значение(максимум).
   
2. 
   Если f ’(x) не меняет знак f(x₀)-f(x)= f ’( ( х₀ -х) -( х₀-δ, х₀) ⇒ f(x₀) >f(x)
   

---

f(x₀)-f(x)= f ’( ( х₀ -х) -( х₀,х₀+­δ) ⇒ f(x₀)

9. 0>
   1   2   3   4   5   6   7   8   9   ...   15

---

Сформулируйте и докажите достаточное условие существования экстремума в терминах второй производной. Опишите условия его применимости и проиллюстрируйте на примере.

В случае когда исследование знака I-ой производной слева и справа от точки x₀ (возможного экстремума) затруднено, целесообразно использовать 2-ое достаточное условие , которое предполагает существование в точке x₀ , конечной II-ой прозводной, отличной от нуля.

Теорема (Второе дост-ое усл-е экстремума в терминах второй пр-ой):

1) Пусть x₀ - стац. точка f(x), т.е. f ′ (x₀) = 0

2) f(x) имеет в т. x₀ конечную 2-ую производную f ′′ (x₀), тогда если f ′′ (x₀) < 0, то в т. x₀ имеем максимум, а если f ′′ (x₀) > 0 , то минимум

Док-во:

По опр-ю производной имеем:f ′′ (x₀) = = =

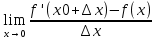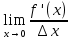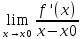
1) По условию f ′′ (x₀) > 0 , функция ( по теореме о пределах) приобретает знак своего предела, то есть функция 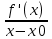приобретает знак своего предела,то есть знак f ′′ (x₀) . f ′′ (x₀) > 0 ,тогда 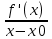, слева от т x₀ , x-x₀ <0, тогда f ′ (x) должно быть меньше 0, чтобы 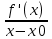> 0 . Справа от т. x_{0 ,} x - x₀ >0 , тогда f ′ (x) должна быть больше 0 , чтобы 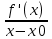> 0 → (по теореме 3) в т. х₀ имеем минимум. ч.т. д.

Правило

Если f ′′ (x₀) > 0 , то имеем в т. х₀ -минимум, а если f ′′ (x₀) < 0 , то имеем в т. х₀ -максимум

Это правило имеет более узкий круг применения. Оно не применимо к тем точкам, где не существует I-ой конечной производной. Не применимо к тем точкам , где II-ая производная равна нулю.

9. Сформулируйте теорему, выражающую достаточные условия экстремума функции, не дифференцируемой в данной точке. Приведите пример.

---

Экстремум функции, не дифференцир-ой в данной точке

Теорема 5.

Пусть f(x) дифференц-ма всюду в некоторой окрестности т х0 , кроме самой т. х0, в которой она однако непрерывна. Тогда,если слева от т. х0 f ′ (x) > 0 (соответственно f ′ (x) < 0 ), а справа от т. х0 f ′ (x) < 0 (соответственно f ′ (x) > 0 ), то т. х0 максимум (соотв-но минимум).

Пример 1. у= ǀ х ǀ - исследовать на экстремум.

1) х >0 , y= x, тогда у′ =1 > 0 (справа от т. 0 )

2) x<0 , y= -x, тогда у′ = - 1 < 0 (слева от т. 0 )

(по теореме 5) в т. х0 = 0 у = ǀ х ǀ - имеет минимум

9. Введите понятия точки возрастания и точки убывания функции. Сформулируйте достаточные условия экстремума в терминах высших производных. Объясните процесс исследования функции на экстремум с помощью высших производных. Приведите пример.

Пусть f(x) определена в некоторой окрестности точки х0, тогда точка х0 называется точкой возрастания(убывания) функции, если существует такое δ>0 что при х0- δ<x<x0 (т.е. слева от точки х0) f(x)>f(x0), а справа от т.х0 при х0<x<x0+ δ f(x)<f(x0),

Точка возрастания -характеризуется тем, что при переходе через неё приращение функции f меняет знак с - на + . Точка убывания с + на -

Достаточные условия экстремума в терминах высших производных

Пусть в т. х0 у функции f(x) существуют все производные до порядка n включительно, причем:

f ′ (x₀) = f ′′ (x₀) = f ′′′ (x₀) = ... = f^(n-1) (x₀ ) = 0 , a f⁽ⁿ⁾ (x₀ ) 0

Тогда, если n - четное, то в т. х₀ есть экстремум, а именно если f^(2k) (x₀ ) > 0 , то минимум , а если f^(2k) (x₀ ) < 0 , то максимум.

Если n – нечетное, то в т. х₀ экстремума нет, а т. х₀ будет точкой возрастания (убывания), если f ^2k+1 (x₀ ) > 0 (f ^2k+1 (x₀ ) < 0 )
Если f ′ (x

---