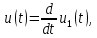Файл: Учереждение высшего профессионального образования московский государственный университет приборостроения и информатики.docx

б) прямоугольного импульса

Определим спектральную плотность амплитуд пря­моугольного импульса, изображенного на (рис. 4.17), если 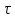= 1 мс, U = 10 В.

Комплексную спектральную плотность прямо­угольного импульса (рис. 4.17) определим, используя прямое преобразование Фурье (4.27):




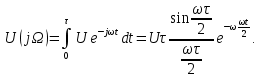
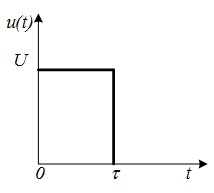
Рис. 4.17. Прямоугольный импульс

Полученное выражение 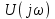отличается от комплексной спектральной плотности (4.35) прямо­угольного импульса, изображенного на (рис. 4.14), множителем 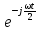, учитывающим запаздывание сигнала (рис. 4.17) на 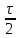и влияющим только на спек­тральную плотность фаз.

Спектральная плотность амплитуд – это модуль комплексной спектральной плотности, поэтому

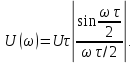
Обратим внимание на то, что спектральная плот­ность амплитуд 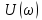прямоугольных импульсов, изображенных на рис. 4.14 и 4.17, рассчитывается по одной и той, же формуле. Это означает, что графики спектральной плотности амплитуд импульсов также совпадают (рис. 4.16, а).

Построим график 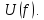Для этого прежде всего рассчитаем значение спектральной плотности ампли­туд на нулевой частоте, которое равно площади пря­моугольного импульса: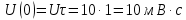



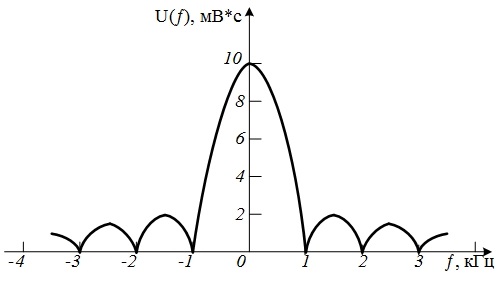
Рис. 4.18. Спектральная плотность амплитуд прямоугольного импульса

Частоты f, на который спектральная плотность обращается в нуль, можно найти из соотношения

---

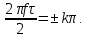
Эти частоты равны 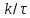, т.е. 1; 2; 3 кГц и т.д. На частотах 1,5 и 2,5 кГц лепестки функции U(f) при­нимают максимальные значения, равные соответст­венно 2 и 1,3 мВ-с. График спектральной плотности амплитуд приведен на рис. 4.18.

Найдем комплексную спектральную плотность тре­угольного импульса, изображенного на рис. 4.19, на частоте f = 200 Гц, если U = 10 В, 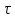 = 5 мс.

Сигнал u(t) можно записать следующим образом:

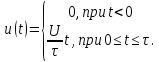
Комплексную спектральную плотность импульса (рис. 4.19) рассчитываем, используя формулу (4.27):
.
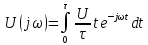Берем интеграл по частям и получаем
.
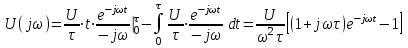На частоте f = 200 Гц комплексная спектральная плотность

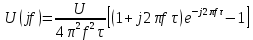
равна 8 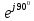, т.е. спектральная плотность амплитуд рав­на 8 мВ·с, а спектральная плотность фаз равна 90°.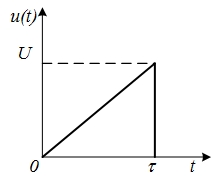



Рис. 4.19. Треугольный импульс

Из прямого преобразования Фурье легко определить спек­тры типовых, часто встречающихся в технике импульсов. Рас­смотрим некоторые из них.

Импульс включения. При анализе переходных процессов в электрических цепях используется импульс включения (единичная функция) (рис. 4.20), который возникает при подключении к це­пи источника постоянного напряжения:

---

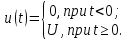
Строго говоря, эта функция не удовлетворяет условиям ин­тегрирования по Фурье, поэтому воспользуемся следующим при­емом: умножим ее на «гасящий» множитель 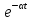, а затем после интегрирования перейдем к пределу при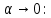
.

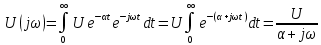Совершая предельный переход, получаем спектральную плот­ность импульса включения:




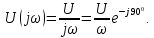
Рис. 4.20. Импульс включения



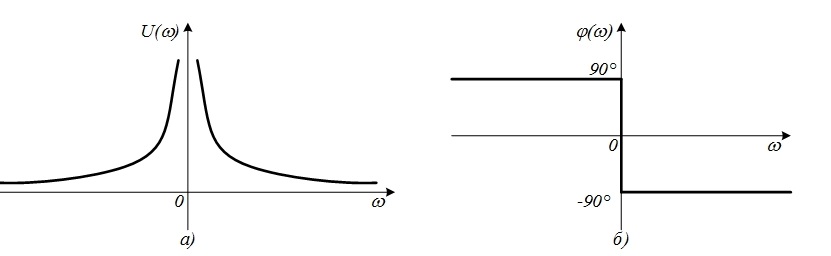
Рис. 4.21. Спектры амплитуд (а) и фаз (б) импульса включения

Спектральная плотность амплитуд при этом 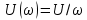, а спектральная плотность фаз 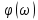= -90°. График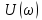и и 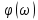показаны на рис. 4.21.

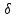-импульс. Этот импульс является математической моделью очень узкого и большого по амплитуде импульса (рис. 4.22, а):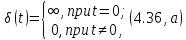

удовлетворяющему условию
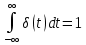, (4.36,б)
т.е. площадь его равна единице.

Для нахождения спектра -импульса воспользуемся прямым преобразованием Фурье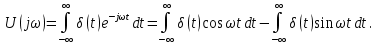



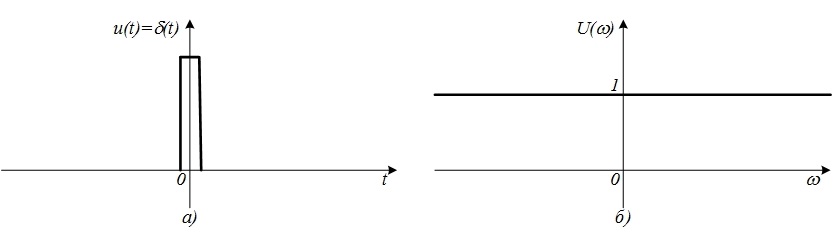
Рис. 4.22. 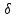-импульс (a) и его спектр (б)

Так как второе слагаемое равно нулю (в силу нечетности по­дынтегрального выражения), то


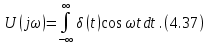
В силу свойства (4.36, а) -импульса подынтегральное выра­жение существует только при

---

t = 0, а это означает, что согласно (4.36, б) 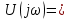1. График спектра -импульса приведен на рис. 4.22, б.

Обратное преобразование Фурье для -импульса имеет вид

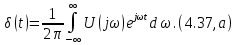
Так как спектр -импульса 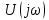= 1, то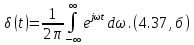



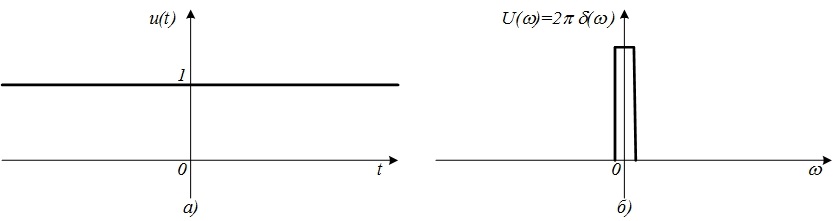
Рис. 4.22. Постоянное напряжение (а) и его спектр (б)

Постоянное напряжение U = 1 В существует во все момен­ты времени, а не только при t ≥ 0.

Учитывая взаимозаменяемость параметров t и 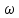, выраже­ние (4.37, б) можно переписать в виде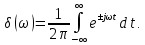

Сравнивая его с выражением для спектра постоянного на­пряжения

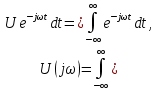
приходим к выводу, что =

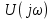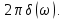
Таким образом, спектр постоянного напряжения (рис. 4.23, б) равен нулю на всех частотах, кроме 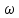= 0, где 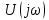обращается в бесконечность.

Экспоненциальный импульс. Переходные процессы в цепях с одним реактивным элементом описываются экспоненциальной функцией (рис. 4.24, а)

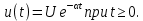
Спектральная плотность этого импульса

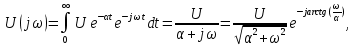
где спектр амплитуд


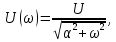
а спектр фаз

---

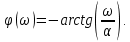
Графики и 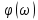показаны на рис. (4.24, б и в).



Рис. 4.24. Экспоненциальный импульс (а) и его спектры амплитуд (б) и фаз (в).

Для вычисления спектров при различных преобразованиях сигналов можно воспользоваться теоремами о спектрах. Остановимся на физической интерпретации основных теорем спек­трального анализа.

Спектр суммы сигналов (теорема линейности). Если сигналы, спектры которых известны, суммируются, то для вычисления ре­зультирующего спектра можно воспользоваться теоремой линейно­сти: спектр суммы сигналов равен сумме спектров этих сигналов.

Итак, если

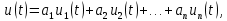
то
.
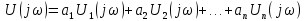Сдвиг сигнала во времени (теорема запаздывания). Часто при обработке сигнала приходится осуществлять его задержку на время :

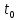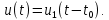
В этом случае спектр задержанного сигнала умножается на множитель :

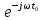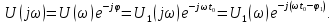
При запаздывании сигнала на время 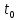его спектральная плотность амплитуд остается неизменной, а спектральная плотность фаз изменяет свой наклон на величину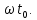

Дифференцирование и интегрирование сигнала. Если сиг­нал 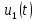подвергается дифференцированию,

---