Файл: Учереждение высшего профессионального образования московский государственный университет приборостроения и информатики.docx

г). В спектре такого сиг­нала вместо отдельных гармоник будет бесконечно большое число синусоидальных колебаний с бесконечно близкими частотами и бесконечно малыми амплитудами. Другими словами, в любой бесконечно узкой полосе частот есть синусоидальное колебание бесконечно малой амплитуды.

Сравнивать между собой бесконечно малые величины не­удобно, поэтому вместо амплитуд 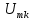(рис. 4.12) по оси ординат откладывают величину ( 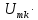Т)/2, которая при увеличении пе­риода Т остается неизменной. Введем новые обозначения для осей ординат на рис. 4.13: U( 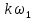) =   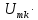(Т/2). В новых коорди­натах спектры сигналов (рис. 4.11) выглядят так, как показано на рис. 4.13, а–г. Спектр непериодического сигнала является в об­щем случае не дискретным, а непрерывным (сплошным).

Для комплексного спектра введенное на рис. 4.13 обозначение примет вид:

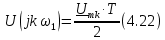
Ранее была получена пара преобразований (4.19) и (4.11) ,позволяющих найти спектр периодического сигнала 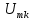и вос­становить периодический сигнал u(t) по его спектру: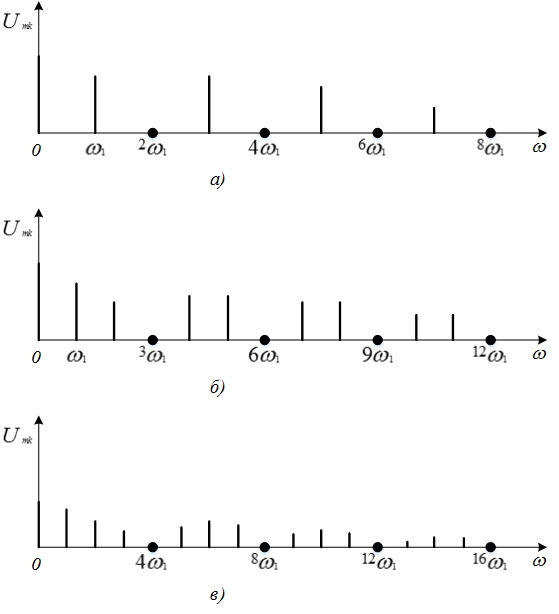


Рис. 4.12. Спектры амплитуд периодических последовательностей импульсов с разными периодами

---

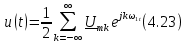
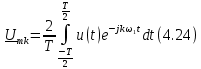
Получим подобную пару преобразований для непериодическо­го сигнала, изображенного на рис. 4.11, г. Для этого нужно в вы­ражении (4.24) устремить период Т к бесконечности и совершить в формулах (4.23) и (4.24) предельные переходы.

Сначала выразим из (4.1) комплексную амплитуду 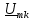в ви­де 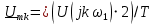и подставим ее в (4.23) и (4.24). Перепи­шем теперь эти выражения в виде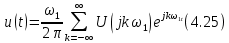

и

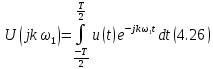
В выражении (4.25) учтено, что Т = 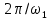. Затем устремим период к бесконечности (Т 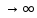). Гармоники будут сгущаться и дискретная частота 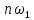перейдет в текущую частоту 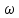, а значе­ние частоты первой гармоники 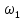будет стремиться к бесконечно малой величине d .

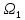После предельного перехода получаем из (4.25) и (4.26)


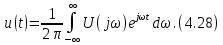
Уравнения (4.27) и (4.28) являются основными в теории спек­тров непериодических сигналов, причем (4.27) называется пря­мым, а (4.28) -обратным преобразованием Фурье (интегралом Фурье). Взаимное преобразование Фурье символически обозначается , где ≓ - знак соответствия этого преобразования.

Если вместо частоты ω использовать частоту f, то эти урав­нения примут вид.

---

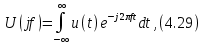
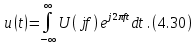
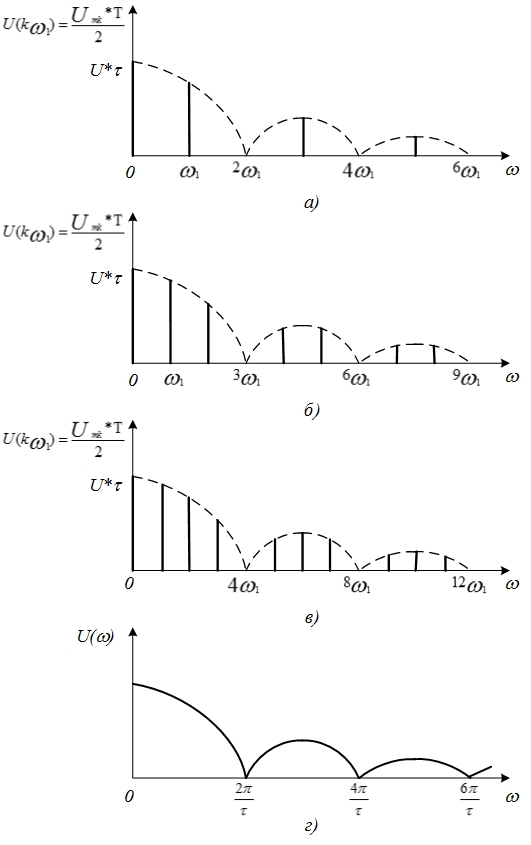
Рис. 4.13. Переход к спектральной плотности прямоугольного импульса

Основные положения изложенных в п. 4.4 материалов:

• 
  Сигнал и его Фурье-изображение связаны парой инте­гральных преобразований, называемых преобразованиями Фурье.
  

5. 1   ...   8   9   10   11   12   13   14   15   ...   22

---

Спектральные плотности амплитуд и фаз непериодических сигналов

Величина 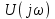в (4.27) или U(jf) в (4.29), называется ком­плексной спектральной плотностью непериодического сигнала u(t).Она может быть записана в показательной и алгебраической формах:
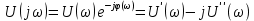(4.31)

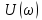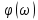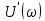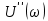и содержит в себе сведения о спектральной плотности ампли­туд и спектральной плотности фаз сигнала, где величины и определяются формулами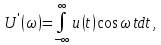





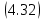
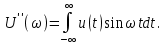
Определим физический смысл преобразования Фурье (4.28). Для этого подставим в выражение (4.28) вместо 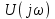его значе­ния из (4.31):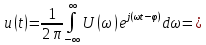



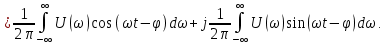
Учитывая, что 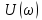– четная, а синус – нечетная функция частоты, интеграл от второго слагаемого равен нулю. Следова­тельно, интеграл Фурье (4.28) имеет вид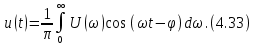

Отсюда следует важнейший вывод о том, что непериодиче­ский сигнал может быть представлен пределом суммы (интег­ралом) бесконечно большого числа гармонических колебаний с бесконечно малыми амплитудами 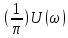и начальными фа­зами 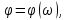причем разность частот соседних гармоник бесконечно мала

---

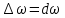: . Это означает, что спектр непериоди­ческого сигнала является сплошным или непрерывным.

Определим спектральную плотность прямоугольного импуль­са, изображенного на рис. 4.14. Для расчета его комплексной спек­тральной плотности воспользуемся







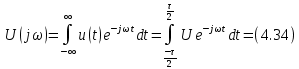
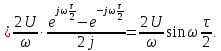
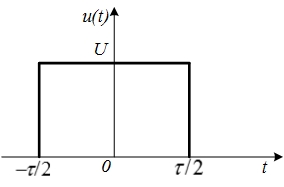
Рис. 4.14. Прямоугольный импульс

Уравнение (4.34) удобнее преобразовать к виду

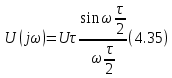
так как это выражение содержит функцию 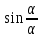, поведение которой хорошо известно: эта затухающая функция максимальна и равна 1, когда 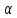=0; она принимает нулевые значения при 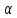= ±k .

График комплексной спектральной плотности прямоугольного импульса изображен на рис. 4.15. В тех областях частот, где функция 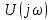положительна, спектральная плотность фаз 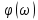равна нулю; там же, где 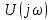отрицательна, спектральная плотность фаз равна ±180°. Поэтому на графиках можно изобра­зить отдельно спектральную плотность амплитуд 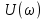– модуль | 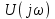| и спектральную плотность фаз 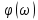(рис. 4.16)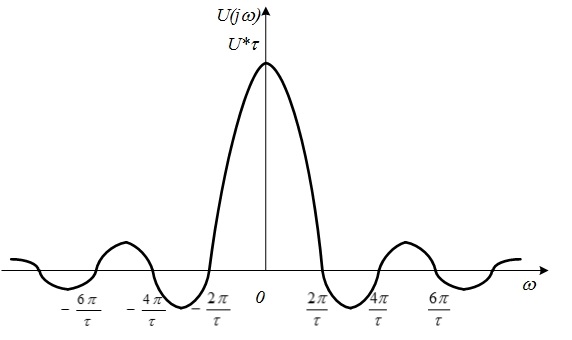


Рис. 4.15. Спектральная плотность прямоугольного импульса



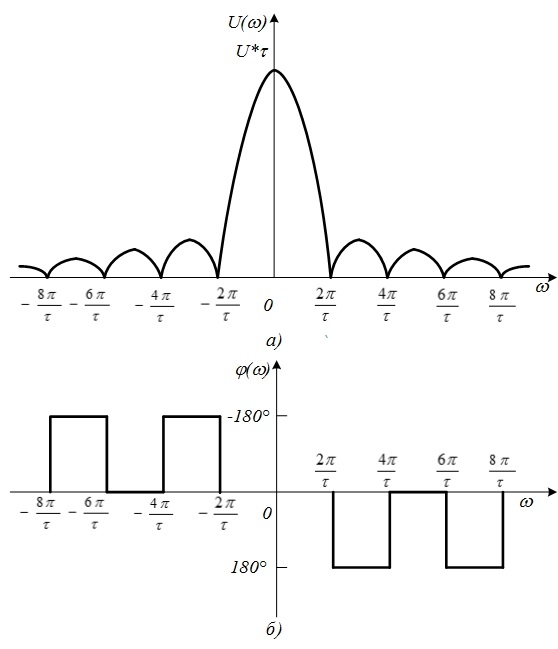
Рис.4.16. Спектральные плотности (спектры) амплитуд (а) и фаз (

---