Файл: Учереждение высшего профессионального образования московский государственный университет приборостроения и информатики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.04.2024
Просмотров: 366
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
Общие сведения об электрических и радиотехнических цепях
Сигналы и их основные характеристики
Корреляционные характеристики детерминированных сигналов
Вопросы и задания для самопроверки:
Методы анализа электрических цепей
Вопросы и задания для самопроверки
Спектры амплитуд и фаз периодических сигналов
Спектральные плотности амплитуд и фаз непериодических сигналов
Примеры определения спектральной плотности сигналов
Определение активной длительности сигнала и активной ширины его спектра
Вопросы и задания для самопроверки:
Комлексная передаточная функция и частотные характеристики цепи
Спектральный анализ цепей при непериодических воздействиях
Вопросы и задания для самопроверки гл. 5, 6:
Вопросы и задания для самопроверки:
Частотный принцип преобразования радиотехнических сигналов
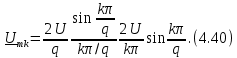
Можно обобщить о преобразовании Фурье сигнала s(t) и его изображения
: -
; -
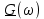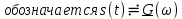функции, сопряженные по Фурье (4.27), (4.28)
-
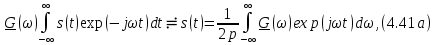
функции, свернутые по времени
-
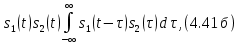
энергия периодического сигнала
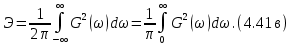
Свойства преобразования Фурье сведены в таблицу 4.2
Таблица 4.2
| № п/ п | Характер, свойство преобразования | Вид колебания 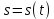 | Спектр 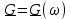 | Примечания |
| 1 | 2 | 3 | 4 | 5 |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | Свойство симметрии Инверсия аргумента функции Свойство линейности Изменение масштаба времени Дифференцирование по времен n- кратное дифференцирование по времени n- кратное дифференцирование по частоте Интегрирование по времени Свойство временного сдвига (теорема запаздывания) Свойство частотного сдвига Умножение на гармоническую функцию Произведение двух функций Свертка функции по времени Автокорреляционная функция (АКФ) Взаимная корреляционная функция АКФ | 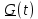 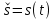 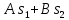 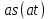 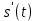 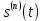 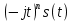 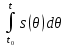 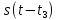 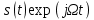 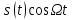 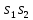 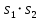 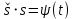 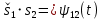 | 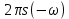 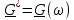 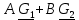 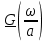 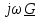 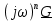 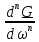 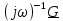 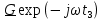 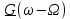 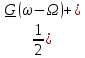 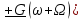 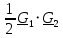 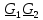 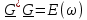 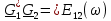 | - 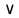 - знак инверсии аргумента - 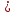знак комплекснойсопряженности A, B – постоянные переменные a – постоянная a>1 – сжатие сигнала и растяжение спектра a<1 – растяжение сигнала и сжатие спектра - - - Результат справедлив, если 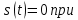 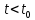 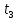 – постоян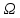ная величина – постоянная величинаПеренос спектра на частоту 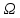- - АКФ и спектр энергии 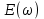 финитного сигнала sВКФ и спектр взаимной энергии 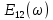 финитных сигналов  |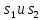
Основные положения изложенных в п. 4.5 материалов:
-
Спектр непериодического сигнала является непрерывным; он состоит из бесконечно большого числа частотных составляющих с бесконечно близкими смежными частотами и с бесконечно малыми амплитудами. -
Чем короче импульс любой формы, тем шире его спектр. -
Запаздывание сигнала приводит лишь к изменению наклона характеристики спектра фаз. -
Для смещения спектра по шкале частот необходимо «заполнить» сигнал гармоническим колебанием. -
Операция свертки сигналов ведет к перемножению их спектров. -
Дискретный спектр «вписывается» в огибающую непрерывного спектра.
- 1>1 ... 9 10 11 12 13 14 15 16 ... 22
Примеры определения спектральной плотности сигналов
Ниже приводится краткое описание некоторых сигналов и определяются их спектральные плотности. При определении спектральных плотностей сигналов, удовлетворяющих условию абсолютной интегрируемости, пользуемся непосредственно формулой (4.41).
Спектральные плотности ряда сигналов приведены в табл. 4.2.
1) Импульс прямоугольной формы (табл. 4.2, поз. 4). Колебание, изображенное на рис. (4.28, а), можно записать в виде
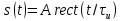.Его спектральная плотность
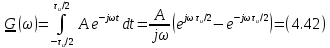
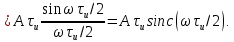
График спектральной плотности
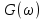(рис. 4.28, а) построен на основе проведанного ранее анализа спектра периодической последовательности однополярных, прямоугольных импульсов (4.14). Как видно из (рис. 4.28, б), функция 
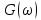обращается в нуль при значениях аргумента 
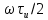= n
, где п - 1, 2, 3, ... — любое целое число. При этом угловые частоты равны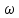 
= 
.
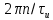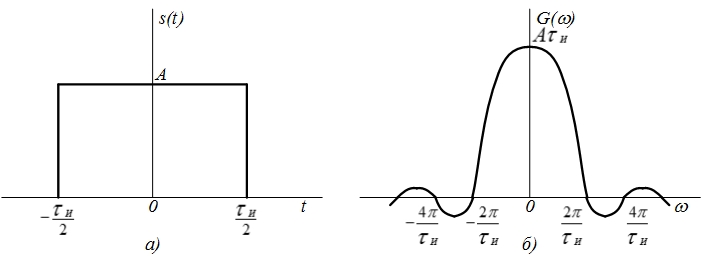
Рис. 4.28. Импульс прямоугольной формы (а) и его спектральная плотность (б)
Спектральная плотность импульса при
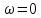численно равна его площади, т.е
G(0)=A
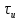. Это положение справедливо для импульса s(t) произвольной формы. Действительно, полагая в общем выражении (4.41) 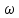= 0, получим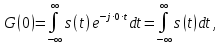
т. е. площадь импульса s(t).
Таблица 4.3.
| № п/п | Сигнал s(t) | Спектральная плотность | ||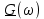
| 1 | 2 | 3 | 4 | 5 |
| 1 |  |  |  |  |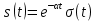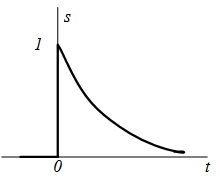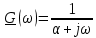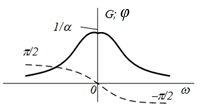
| 2 |  |  |  |  |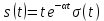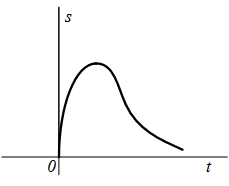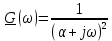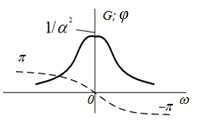
| 3 |  |  |  |  |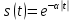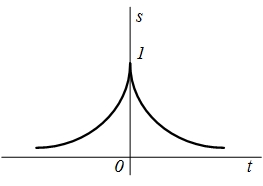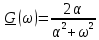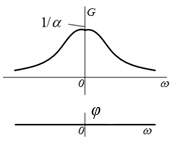
| 4 |  |  |  |  |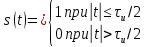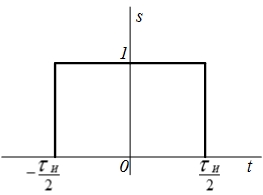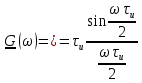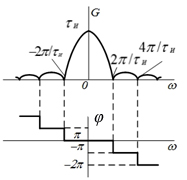
| 5 |  |  |  |  |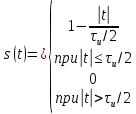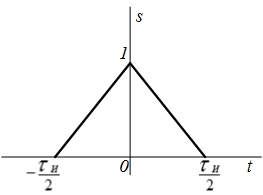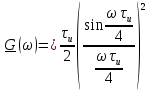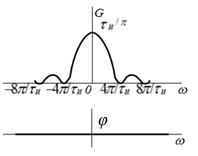
| 6 |  |  |   |  |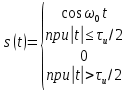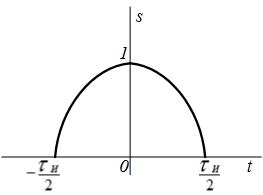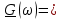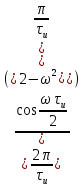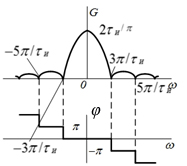
| 7 |  |  |  |  |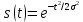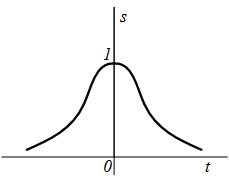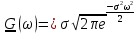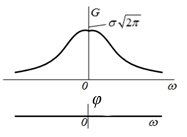
| 8 |  |  |  |  |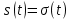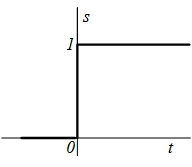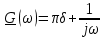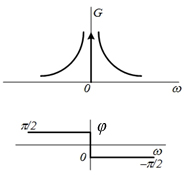
| 9 |  |  |  |  |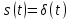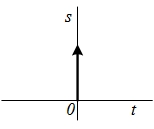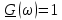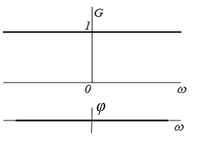
| 10 |  |  |  |  |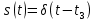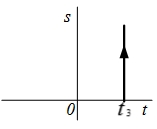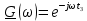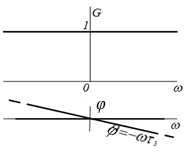
| 11 |  |  |  |  |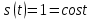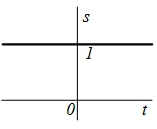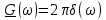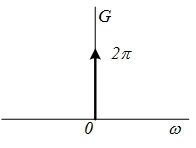
| 12 |  |  |   |  |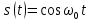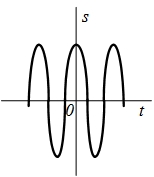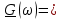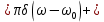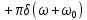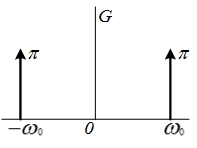
| 13 |  |  |   |  |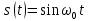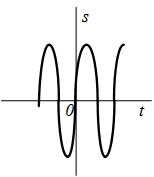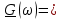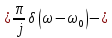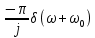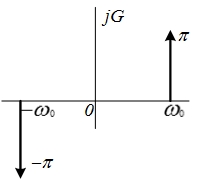
| 14 |  |  |  |  |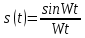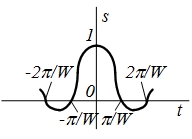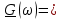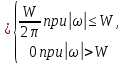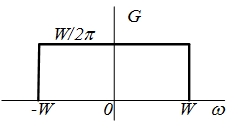
| 15 |  |  |  |  |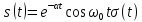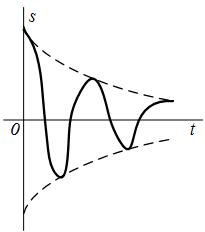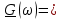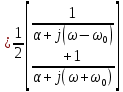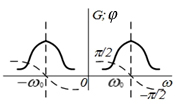
| 16 |  | - |   |  |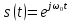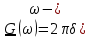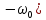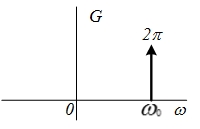
| 17 |  |  |  |  |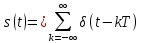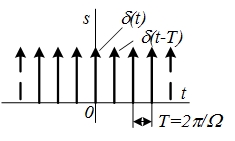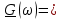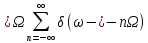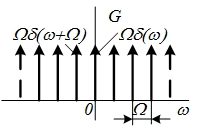
При растягивании импульса расстояние между нулями функции
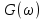сокращается, т. е. происходит сжатие спектра. Значение 
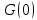при этом возрастает. Наоборот, при сжатии импульса происходит расширение его спектра а значение 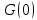уменьшается. На (рис. 4.29, а, б) приведены графики амплитудного 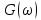и фазового и 
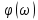спектров прямоугольного импульса.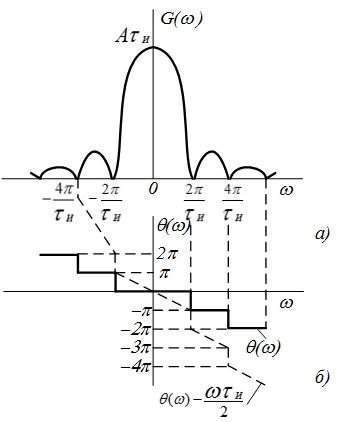
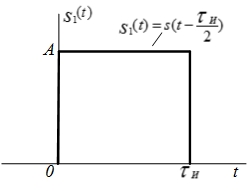
Рис. 4.29. Графики амплитудного (а) Рис. 4.30. Импульс прямоугольной формы, и фазового (б) спектров сдвинутый на время
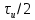
При сдвиге импульса вправо (запаздывание) на время
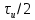(рис. 4.30) фазовый спектр изменяется на величину 
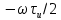, определяемую аргументом множителя exp(
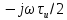) (табл. 4.2, поз. 9). Результирующий фазовый спектр запаздывающего импульса изображен на рис. 4.29, б пунктирной линией.2) Дельта-функция
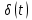(табл. 4.3, поз. 9). Спектральную плотность 
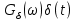– функции находим по формуле (4.41), используя фильтрующее свойство δ-функции: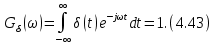
Таким образом, амплитудный спектр
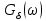равномерный и определяется площадью δ-функции [ 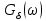= 1], а фазовый спектр равен нулю [ 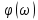= 0].
