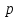Файл: Учереждение высшего профессионального образования московский государственный университет приборостроения и информатики.docx

Вопросы и задания для самопроверки гл. 5, 6:

1. 
   Как определяется комплексная передаточная функция цепи?
   
2. 
   Какие методы используются для расчета реакции цепи на непериодическое воздействие?
   
3. 
   Сформулировать условия безыскаженной передачи сигналов через линейную цепь.
   

7. Представление непериодических сигналов интегралом лапласа

Подстановка оператора 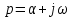вместо jω в интеграл (4.27, 4.28) приводит к следующим выражениям: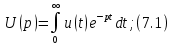


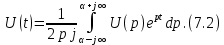
В выражении (7.1) и (7.2) нижние пределы интегрирования взяты равными нулю. Тем самым заранее предполагается, что напря­жения и токи отсутствуют при < 0. Это не слишком жесткое огра­ничение, накладываемое на сигналы, поскольку всегда можно вы­брать такое начало отсчета, ранее которого сигналы не существуют.

Выражение типа (7.1) получило название прямого преобразования Лапласа. Оно позволяет по временной форме сигнала определить его изображение по Лапласу. Выражение (7.2) называется обратным преобразованием Лапласа. Оно дает возможность перейти от изображения к оригиналу, т.е. к временному представлению сигнала.

Для сокращенной записи преобразований (7.1) и (7.2) используют знак соответствия ≓.



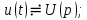
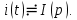
Таблица 7.1. Преобразования Лапласа сигналов, используемых при анализе цепей

---

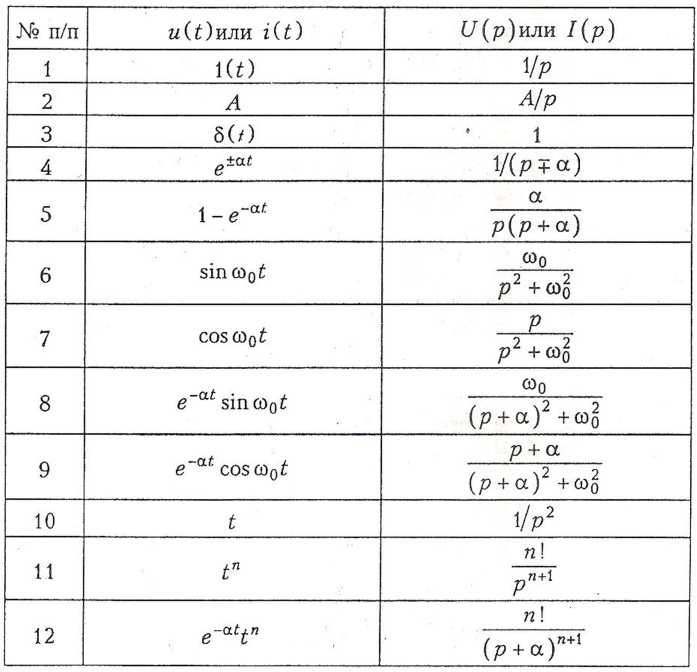
Преобразования Лапласа для простейших функций рассчита­ны и сведены в справочные таблицы. Для теоретических и экспе­риментальных исследований характеристик электрических цепей и передачи сообщений по каналам связи используют испытатель­ные сигналы в форме единичной функции 1(t) и единичной им­пульсной функции ????(t) (функция Дирака), а также гармониче­ские импульсы включения, уровни постоянных напряжений, пря­моугольные импульсы, экспоненциальные сигналы и т.д. Ориги­налы и изображения сигналов, наиболее часто применяемых при анализе электрических цепей, приведены в табл. 7.1.

Определим изображения некоторых функций, оригиналы ко­торых приведены в табл. 7.1.

Пример 1. Найдем изображение напряжения в форме единичной функции 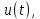которое соответствует включению по­стоянного напряжения, равного 1 В, в момент 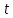= 0.

Напряжение 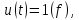изображенное на рис. 7.1, можно представить как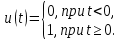

Преобразование Лапласа напряжения u(t) рас­считаем, используя выражение (7.1):

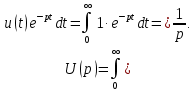
Полученное изображение напряжения в форме единичной функции

соответствует выражению, приведенному в строке 1 табл. 7.1



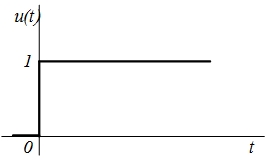
Рис. 7.1. Напряжение в форме единичной функции

Любое произвольное постоянное напряжение, подключенное в момент времени

---

= 0, может быть получено путем умножения единичной функции на соответствующую константу А, т.е. 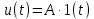. Изображение такого напряжения приведено в строке 2 табл. 7.1: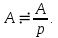

Пример 2. Найдем изображения напряжения в форме экспо­ненциальной функции .

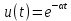Согласно (7.1) изображение экспоненциального напряжения имеет вид

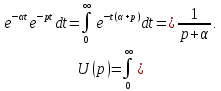
или в сокращенной форме

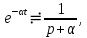
что соответствует выражению, приведенному в стро­ке 4 табл. 7.1.

Найдем изображение тока 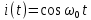. Воспользуемся формулой Эйлера и представим косинусоидальную функцию 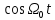в виде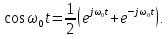

Изображение 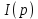гармонического тока полу­чим, используя прямое преобразование Лапласа (7.1) и разложение 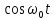на две экспоненциальные функции: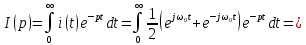



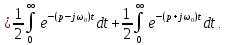
Рассчитав сумму двух приведенных выше интег­ралов, получим

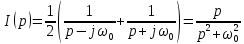
или


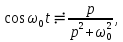
что соответствует выражению в строке 7 табл. 7.1.

Аналогичным образом, используя преобразование Лапласа, можно найти изображения синусоидального и ко­синусоидального

---

сигналов, амплитуды которых затухают по экс­поненциальному закону (строки 8 и 9 в табл. 7.1), единичной импульсной функции

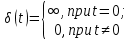
(строка 3 в табл. 7.1), а также типовых сигналов и их комбина­ций (строки 5, 10, 11, 12 табл. 7.1), применение которых будет показано в следующих параграфах.

Свойства преобразований Лапласа. Математическим опе­рациям над оригиналами соответствуют определенные операции над изображениями, называемые свойствами преобразований Лапласа. Они облегчают нахождение изображений сложных сигналов и вычисление искомых оригиналов по найденным изо­бражениям. Свойства преобразований Лапласа применимы к любым сигналам (токам и напряжениям), рассматриваемым в этой главе.

Умножение на константу. Если оригинал , имеющий изображение 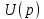, умножается на постоянный коэффициент 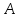, то изображение тоже умножается на этот же самый коэффи­циент: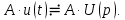


Аналогично


Это свойство легко доказать, взяв преобразование Лапласа (7.1) от функци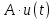и или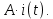

Свойство линейности можно записать в виде

---

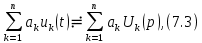
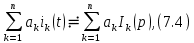
где 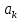— постоянные коэффициенты.

Свойство легко доказать, если применить к левой части пря­мое преобразование Лапласа (7.1)

Приведенные выше формулы означают, что преобразование Лапласа суммы нескольких оригиналов есть сумма преобразова­ний Лапласа каждого из оригиналов.

Пример 3. Найдем изображение напряжения

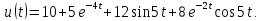
Для нахождения изображения 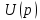воспользуем­ся данными табл. 7.1 (строки 2, 4, 6, 9) и свойствами линейности и умножения на константу. Получим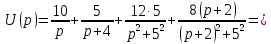



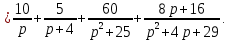
Дифференцирование оригинала (теорема дифференцирования).

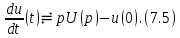
Эта математическая операция означает, что для нахождения пре­образования Лапласа производной от оригинала необходимо изо­бражение оригинала умножить на оператор 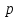и вычесть началь­ное значение оригинала.

Для доказательства подставим 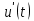в выражение для опре­деления прямого преобразования Лапласа (7.1):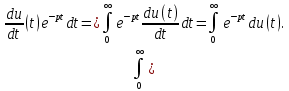


После интегрирования по частям получаем

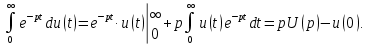
Если начальное значение оригинала равно нулю, т.е. 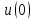= 0, то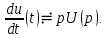

Аналогично


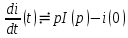
при ненулевых начальных условиях,


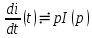
при

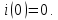
Другими словами, операция дифференцирования во времен­ной области заменяется простой операцией умножения изображе­ния на оператор

---