Файл: 9. Введите понятие производной второго, третьего и т д.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 19.10.2024
Просмотров: 79
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Введем обозначения
Достаточное условие экстремума. Пусть функция
1) если то точка
2) если то в точке
3) если то экстремум может быть, а может и не быть.
Шаг 1. Находим частные производные
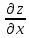 и
и 
Шаг 2. Составляем систему уравнений из равенств этих производных нулю (их равенство нулю и есть необходимый признак существования экстремума):
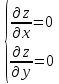
Решения этой системы уравнений (xk: yk) являются точками возможного экстремума - критическими точками.
Шаг 3. Пусть M0(x0; y0) является критической точкой, найденной на шаге 2. Чтобы убедиться, что в ней существует экстремум функции двух переменных, находим частные производные второго порядка
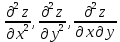
как частные производные от частных производных первого порядка, найденных на шаге 1.
Шаг 4. Присваиваем частным производным второго порядка, найденным на шаге 3, буквенные обозначения:
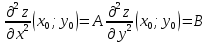
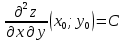
Находим определитель
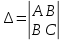 и проверяем достаточный признак существования экстремума.
и проверяем достаточный признак существования экстремума.Если ,
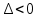 то экстремума в найденной критической точке нет,
то экстремума в найденной критической точке нет,если
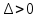 , то экстремум в найденной критической точке есть,
, то экстремум в найденной критической точке есть,если
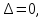 то то требуются дополнительные исследования.
то то требуются дополнительные исследования.Если экстремум в найденной точке есть и если
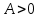 , то в этой точке существует минимум функции двух переменных, если
, то в этой точке существует минимум функции двух переменных, если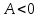 , то максимум.
, то максимум.Шаг 5. Подставляем значения критической точки, в которой найден экстремум, в исходную функцию двух переменных z = z(x; y) и получаем значение экстремума функции двух переменных (минимума или максимума).
Примеры начнём с более сложного, в котором составленная система уравнений имеет несколько решений, а, значит, найдено несколько критических точек.
- Сформулируйте задачу восстановления функции по ее производной. Объясните понятие первообразной функции. Приведите примеры. Докажите основное свойство первообразных. Сформулируйте правила нахождения первообразных и проиллюстрируйте их.
Основная задача дифференциального исчисления: отыскание производной данной функции
Дано: f(x). Найти: f ’(x)
Обратная задача отыскание функции по ее производной (задача восстановления)
Дано: F’(x). Найти: f(x), т.е. восстановить функцию по ее производной. Обратная задача к основной задаче является задачей дифференциального исчисления.
| В дифференциальном исчислении | В интегральном исчислении | ||||||||
|
|
Пусть f(x) определена на некотором промежутке Е (конечный или бесконечный, замкнутый или незамкнутый).Тогда F(x) называется первообразной функцией для f(x) на Е, если F′ (x) = f(x).
Основное свойство первообразных (2 формулировки).
А) Любая первообразная для функции f(x) на промежутке Е может быть представлена в виде: F(x)+С.
Доказательство. Пусть F(x)- первообразная f(x) →(по определению) F′(x)= f(x), пусть Ф(х)- первообразная f(x) →(по определению) Ф′ (x)= f(x).
Докажем, что Ф(х)= F(x)+С.
(Ф(х)– F(x))′ = Ф′ (х)– F′ (x)= f(x)– f(x)=0
Ф(х)– F(x)=С→ Ф(х)= F(x)+С ч.т.д.
Б) Если в некотором Е функция f(x) имеет первообразную F(x), то F(x±С) – также является её первообразной. Доказательство. Пусть F(x)- первообразная f(x) →(по определению) F′ (x)= f(x).
Проверим: (F(x)+С)′ = F′ (x)+C′= f(x)+0= f(x) ч.т.д.
Правила нахождения первообразных.
1) Если F(x)- первообразная f(x), а G(x)- первообразная g(x), то (F(x)+ G(x)) – первообразная для (f(x)+ g(x)). (F(x)+ G(x))′ = F′ (x)+ G′ (x)= f(x)+g(x).
2) Если F(x)- первообразная f(x), а k – постоянная, то kF(x)- первообразная kf(x).
3) Если F(x)- первообразная f(x), а k, b – постоянные, причем k≠0, то
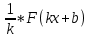 - первообразная для f(kx+b).
- первообразная для f(kx+b). - 1 ... 7 8 9 10 11 12 13 14 15
Введите понятие неопределенного интеграла и объясните его геометрический смысл. Сформулируйте и докажите основные свойства неопределенного интеграла.
Если F(x)-первообразная функции f(x) на промежутке Е, то F(x)+C, где С-произвольная постоянная называется неопределенным интегралом от функции f(x).
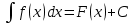 , где f(x)dx называется подынтегральным выражением, функция f(x) - подынтегральной функцией.
, где f(x)dx называется подынтегральным выражением, функция f(x) - подынтегральной функцией.Геометрический смысл неопределенного интеграла
Геометрически, неопределенный интеграл представляет собой семейство интегральных кривых на плоскости, полученных путем параллельного переноса графика функции y=f(x) вдоль оси ординат (рис. 3).
Основные свойства неопределённого интеграла
Свойство 1. Производная неопределенного интеграла равна подынтегральной функции:
Доказательство.
Свойство 2. Дифференциал неопределенного интеграла равен подынтегральному выражению:
Доказательство.
Свойство 3. Неопределенный интеграл от дифференциала функции равен этой функции плюс const:
Доказательство.
Свойство 4.Неопределенный интеграл от алгебраической суммы функций равен алгебраической сумме неопределенных интегралов от этих функций:
Доказательство. пусть F(x) и G(x) – первообразные для функций f(x) и g(x) соответственно, т.е.
.
Следовательно,
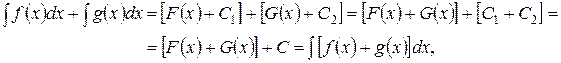 где – произвольная постоянная. Отметим, что данное свойство справедливо для любого конечного числа слагаемых функций.
где – произвольная постоянная. Отметим, что данное свойство справедливо для любого конечного числа слагаемых функций.Свойство 5.Постоянный множитель можно выносить за знак интеграла:
Доказательство. пусть F(x) – первообразная для функции f(x) , т.е.
Отсюда следует, что
- Опишите основные методы вычисления неопределенного интеграла. Приведите примеры. Объясните, в каких случаях применяется метод интегрирования по частям и метод подведения под знак дифференциала. Что означает приведение интеграла к самому себе?
Интегрирование с помощью замены переменной (или интегрирование подстановкой).
Теорема. Пусть функции f(u), и u = ϕ(x) определены на некоторых интервалах так, что имеет смысл сложная функция f(ϕ(x)) и функция ϕ(x) непрерывно дифференцируема. Тогда, если функция f(u) имеет первообразную F(u), то есть существует: ∫f(u)du =F(u) + C, то функция f(ϕ(x)) имеет первообразную F(ϕ(x)) и, значит, ∫ f(ϕ(x))*ϕ′(x)dx = F(ϕ(x)) + C.
∫ f(ϕ(x))*ϕ′(x)dx = ∫f(u)du – интегрирование подстановкой.
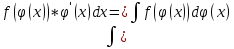 – формула подведения под знак дифференциала.
– формула подведения под знак дифференциала.Интегрирование по частям.
Теорема. Если функции u(x) и v(x) дифференцируемы на некотором промежутке и существует интеграл ∫u*du, то существует и интеграл ∫u*dv, справедливо равенство:
∫ u*dv = u*v− ∫ v*du
Доказательство.
Вычислим дифференциал произведения функций u(x)*v(x). d(u(x)*v(x)) = v(x)du(x) + u(x)dv(x) или u(x)dv(x) = d(u(x)*v(x))−v(x)du(x). Если дифференциалы функций равны, то, очевидно, их неопределенные интегралы, как множества функций, совпадают; поэтому ∫ u(x)dv(x) =∫ d(u(x)*v(x))− ∫ v(x)du(x).
Основные группы интегралов, которые берутся посредством интегрирования по частям.
