Файл: Учереждение высшего профессионального образования московский государственный университет приборостроения и информатики.docx

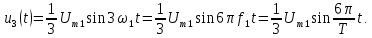
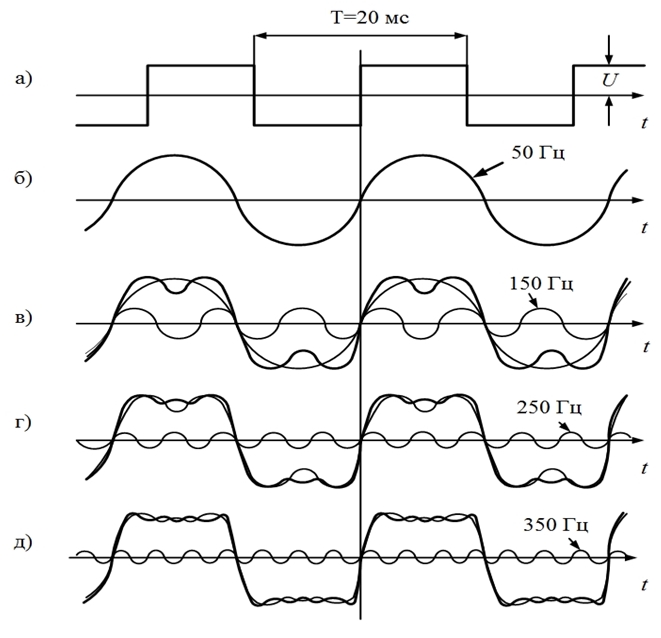
Рис. 4.1. Последовательность прямоугольных импульсов и образующие ее синусоиды

Сумма этих двух синусоид, т.е. 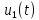+ u₃(t), пока еще мало похожа на прямоугольные импульсы (рис. 4.1, в). Но если мы добавим к ним синусоиды с частотами в 5, 7, 9, 11 и т.д. раз большими, то сумма всех этих колебаний
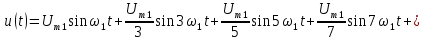(4.3)


будет не так уж сильно отличаться от прямоугольных импульсов (рис. 4.1, г и д). Таким образом, из (4.3) следует, что в случае последовательности прямоугольных импульсов, симметричной относительно начала координат, ряд Фурье (4.2) состоит толь­ко из синусоидальных колебаний.

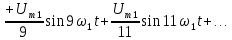
Ниже мы покажем, что для того, чтобы сигнал, сформирован­ный из синусоид (4.3), совпадал с прямоугольными импульсами также и по высоте, амплитуду основной синусоиды следует взять

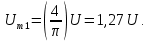
Таким образом, степень прямоугольности импульсов определя­ется количеством синусоид со все более высокими частотами, которые мы будем суммировать в (4.3).

Построения на рис. 4.1 носят скорее наглядный характер. Воспользовавшись формулами (4.2), можно выполнить точные вычисления.

Постоянная составляющая ряда Фурье

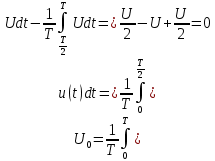
равна нулю, т.е. она в данном сигнале отсутствует.

Амплитуды косинусоидальных гармоник




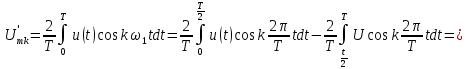
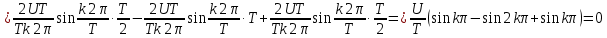
также равны нулю при любых значениях k, что означает их от­сутствие в сигнале.

Амплитуды синусоидальны составляющих ряда Фурье

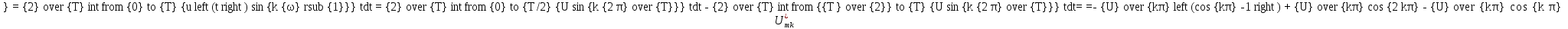
При k=1

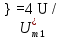
k=2

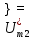
k=3

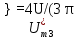
k=4

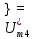
k=5

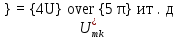
Амплитуда 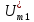, обозначена в формуле (4.3) как амплитуда первой (основной) гармоники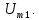

Может показаться, что представление периодических сигна­лов в виде совокупности гармоник есть не более чем математиче­ский прием и не имеет никакого отношения к реальности. Однако это не так. Если бы вам удалось, например, подобрать струны с частотами колебаний, кратными числам 1, 3, 5, 7, ..., и распо­ложив их рядом друг с другом, привести одновременно в движе­ние так, чтобы амплитуды колебаний струн соотносились как: (1/3) : (1/5) : (1/7) ..., то вы бы увидели, что форма кривой звукового давления, создаваемого этими струнами совместно (а значит, и форма тока, например, в цепи микрофона), была бы прямоугольной.

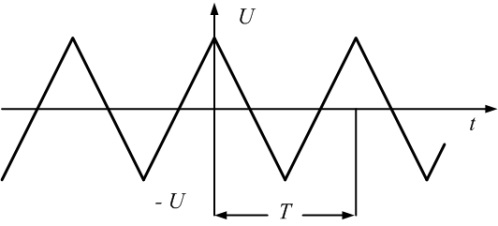
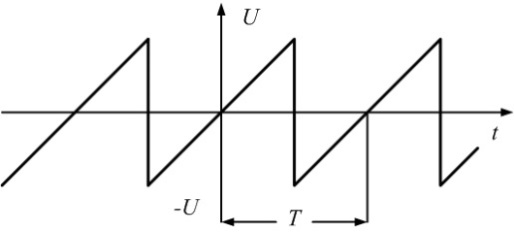
Другим примером периодических несинусои­дальных колебаний может служить сигнал пилообразной формы (рис. 4.2, а).

Пилообразный сигнал, симметричный относительно начала координат, также состоит только из синусоид. Чтобы сформировать пилообразный сигнал, нужно взять сна­чала основную синусоиду или первую гармонику (рис. 4.2, б):

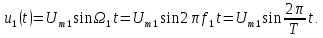
Амплитуду этой гармоники можно рассчитать по формуле (4.2). Она равна

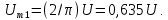
Затем следует использовать перевернутую синусоиду удвоенной частоты и половиной амплитуды (рис 4.2,в):

а также синусоиды с утроенной, учетверенной и т.д. частотами (рис. 4.2, г-е):
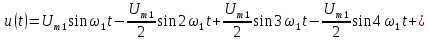(4.4.)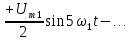


Изменение начала координат превращает ряд, состоящий из синусов, в косинусный ряд. Покажем на примере последователь­ности прямоугольных импульсов, как изменение начала коорди­нат превращает ряд, состоящий из синусов, в ряд, состоящий из косинусов.

Рисунок 4.3, а отличается от рис. 4.1, а незначительно: мо­мент наблюдения (т.е. начало координат) смещен вправо на чет­верть периода последовательности прямоугольных импульсов.


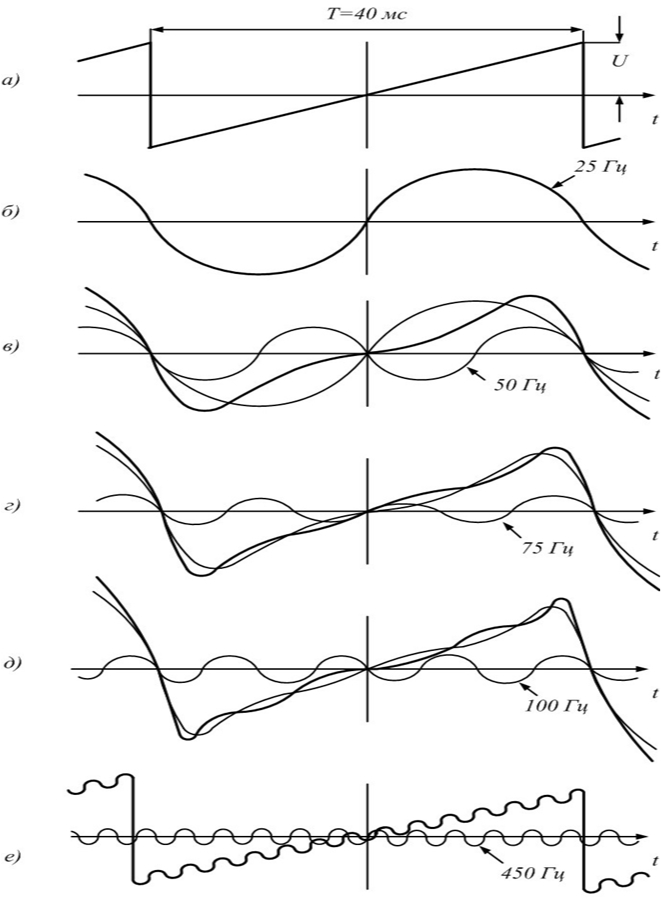
Рис.4.2. Последовательность пилообразных импульсов и образующие ее синусоиды

Напомним, что колебание, которое начинается раньше нача­ла координат, называется опережающим по отношению к коле­банию, возникающему из начала координат, и характеризуется появлением начальной фазы со знаком «плюс». Это означает, что теперь вместо колебания (4.1, б) мы будем иметь дело с коле­банием, опережающим по фазе данное колебание на /2 рад или на 90° (рис. 4.3,б):

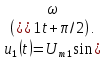
Колебание утроенной частоты 3 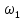после переноса начала ко­ординат получит сдвиг по фазе, равный З /2 рад, или 270° (рис. 4.3, в):

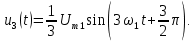
Продолжая действовать таким образом, мы придем к форму­ле для последовательности прямоугольных импульсов:

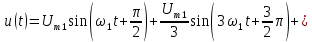(4.5)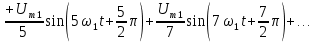





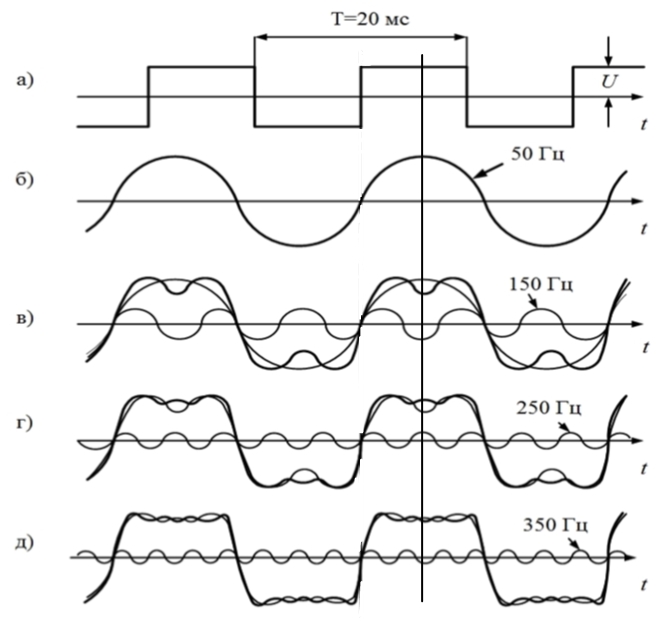
Рис.4.3. Последовательность прямоугольных импульсов, смещенная на 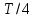относительно начала координат.

Применив к (4.5) тригонометрические формулы приведения

sin(

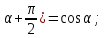
sin

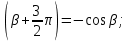
sin(

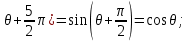
sin( ;

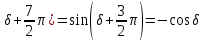sin( 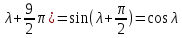; и т.д.

можно представить ряд (4.5) в виде суммы только косинусоид.

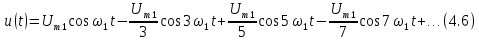
Периодические сигналы любой формы также состоят из суммы синусоид или косинусоид; при этом нечетные сигналы состоят только из синусоид, в то время как четные сигналы — только из косинусоид.

В табл. 4.1 приведены наиболее часто встречающиеся на практике периодические последовательности импульсов и записаны их представления в виде синусных или косинусных рядов. Из таблицы видно, что нечетные функции содержат только синусоиды, а четные — только косинусоиды. Напомним, что четной называется функция, удовлетворяющая соотношению x(-t) = x(t),нечетной — удовлетворяющая соотношению x(-t) = -x(t).
Таблица 4.1. Ряды Фурье наиболее часто встречающихся сигналов

Сигнал	Ряд Фурье
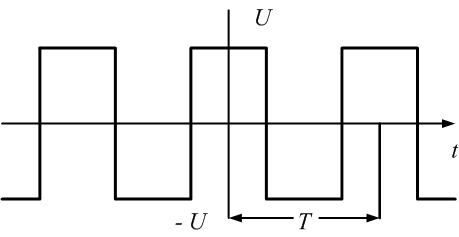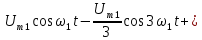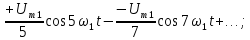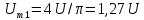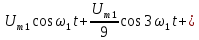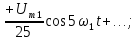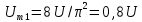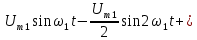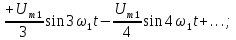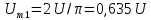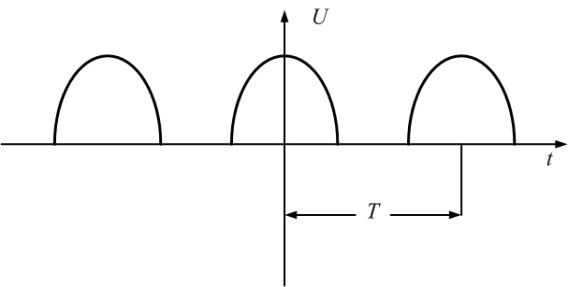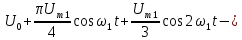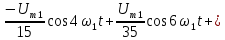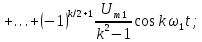	k-четные;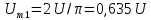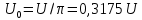
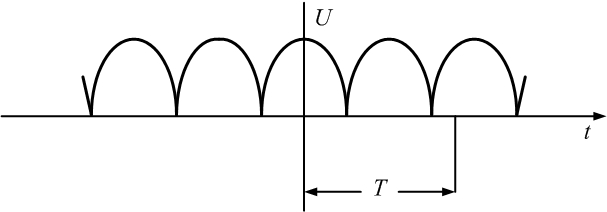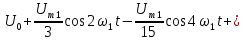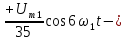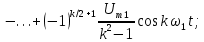	k-четные;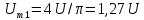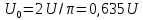
	; ;

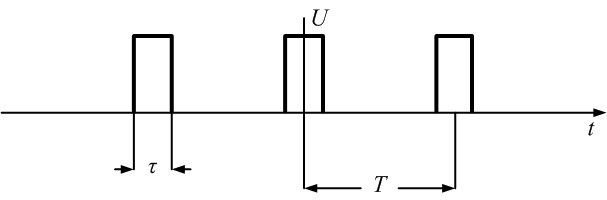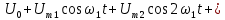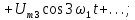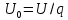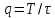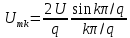В честь французского математика приведенные в таблице ряды называются рядами Фурье. Наинизшая частота синусоидальных или косинусоидальных компонент есть
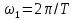или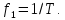
Эта частота принадлежит основной составляющей, и она сов­падает с частотой повторения сигнала. Таким образом, периодический сигнал с периодом в 1 мс имеет основную составляющую с частотой

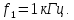
Частоты остальных составляющих сигнала являются числами, кратными частоте основной составляющей. Эти составляющие называются гармониками основной компоненты, и номер гармоники определяется отношением ее частоты к частоте основной составляющей. Так, в приведенном в предыдущем абзаце примере гармониками основной составляющей в общем случае могут быть вторая – с частотой 2 кГц, третья – с частотой 3 кГц, четвертая – с частотой 4 кГц и т.д.

Гармоники в ряде Фурье можно вы­делить и измерить с помощью измерительного прибора – анализато­ра спектра. Простейшая схема такого анализатора в качестве основ­ного элемента включает полосовой фильтр с высокой избирательностью и перестраиваемой центральной частотой. К вы­ходным зажимам фильтра подключается чувствительный индикатор: милливольтметр или осциллографическая трубка. Центральная часто­та фильтра, как правило, перестраивается автоматически. При совпа­дении частоты гармоники, содержащейся во входном сигнале, с цен­тральной частотой фильтра индикатор показывает амплитуду отдельной гармоники ряда Фурье.

Кроме основной составляющей и высших гармоник в сигна­ле может присутствовать постоянная составляющая. Посмотрите на рис. 4.4, а и б. Нижний рисунок получен из верхнего вычита­нием среднего значения сигнала, которое вычисляется, как из­вестно, по формуле

Для последовательности прямоугольных импульсов, изобра­женной на рис. 4.4, а, указанную площадь вычислить нетрудно, поэтому

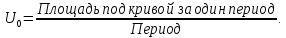
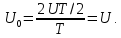
В случае, когда сигнал имеет сложную форму, площадь вы­числяется с помощью интеграла из формулы (4.2):

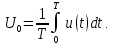
Среднее значение сигнала 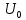называют постоянной состав­ляющей. Удаление постоянной составляющей из последователь­ности прямоугольных импульсов на рис. 4.3, а приводит к после­довательности, показанной на рис. 4.4, б.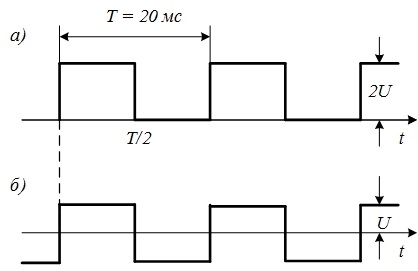



Рис. 4.4. Последовательности прямоугольных импульсов

Поскольку гармонический состав последнего сигнала известен (4.3), то гармонический состав однополярной последовательности импульсов (рис. 4.4, а) будет отличаться только наличием посто­йной составляющей :

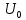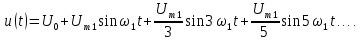
В двух предпоследних строках табл. 4.1 можно увидеть постоянные составляющие у переменного напряжения, выпрямленного одно- и двухполупериодным выпрямителями.

Общая форма записи ряда Фурье содержит амплитуды и начальные фазы гармоник. Мы наблюдали ранее, как изменение начала координат (т.е. момента начала наблюдения) превращало ряд синусов в ряд косинусов. Так, при переносе начала координат на рис. 4.1, а вправо на четверть периода последовательности прямоугольных импульсов (т.е. при переходе к рис. 4.3, а) изменились начальные фазы основной составляющей и высших гармоник на величины, кратные /2 рад (4.5).

Очевидно, если начало координат переносить на произвольное расстояние вправо или влево, то начальные фазы основной составляющей и гармоник в (4.5) будут принимать любые значения, а не только кратные /2 рад. В этом случае ряд (4.5) преобразуется в ряд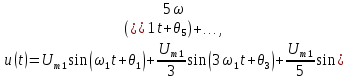

где 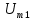= 1,27U; 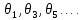- начальные фазы первой, третьей, пятой и т.д. гармоник.

Каждый сигнал, отличающийся от других по форме, имеет сугубо индивидуальный гармонический состав, т.е. содержит основную синусоиду и ее высшие гармоники со своими амплитудами и начальными фазами. Поэтому в общем случае ряд Фурье произвольного периодического сигнала записывается в форме



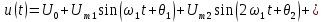
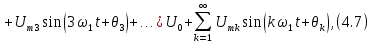
U_mk –амплитуды k-й гармоники; 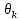— начальная фаза k-й гармоники.

Мы уже знаем, что амплитуды некоторых гармоник могут быть равны нулю, а фазы могут принимать любые значения, в числе и кратные /2 рад — это зависит от формы сигнала (см. табл. 4.1).

Форма записи ряда Фурье (4.7) получила название синусоидальной тригонометрической. Она справедлива для любого момента наблюдения, т.е. для любого расположения начала координат, и широко используется в электротехнике.

Существуют две равноправные записи ряда Фурье в тригонометрической форме — через функцию синуса и через функцию косинуса. Ряд Фурье с использованием функции синуса мы записали в виде формулы (4.7). Чтобы заменить функцию синуса на функцию косинуса нужно учитывать сдвиг фаз между функциями sin и cos: 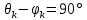. Таким образом: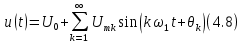



и


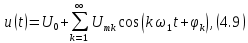
где угол k-й гармоники 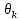отсчитывается от положительной горизонтальной оси, а угол 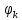от положительной вертикальной оси комплексной плоскости.

Чтобы избежать путаницы, примем в дальнейшем в качестве основной формы записи ряда Фурье формулу (4.9) и, кроме то будем иметь дело не с угловой частотой 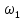а с линейной частотой 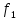в Гц, кГц, МГц, устанавливаемой на шкалах реальных зрительных приборов, так что ряд Фурье будет иметь вид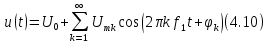



Уравнение (4.10) есть косинусоидальная тригонометрическая форма ряда Фурье, и она широко используется в радиотехнике.

При анализе цепей часто удобно пользоваться комплексной формой ряда Фурье, которая может быть получена из (4.10) с помощью формулы Эйлера иодной суммой дает запись ряда Фурье в комплексной форме:


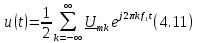
Основные положения изложенных в п. 4.1 материалов:

• 
  Периодическая последовательность прямоугольных пилооб­разных, треугольных и других импульсов состоит из сину­соид кратных частот.
  
• 
  Изменение начала координат может превратить ряд, со­стоящий из синусоид, в косинусный ряд.
  
• 
  Периодические сигналы любой формы также состоят из си­нусоид или косинусоид; при этом нечетные сигналы состоят только из синусоид, в то время как четные сигналы — толь­ко из косинусоид.
  

• 
  Кроме основной составляющей и высших гармоник в сиг­нале может присутствовать постоянная составляющая.
  
• 
  Существуют две равноправные записи ряда Фурье в триго­нометрической форме — через функцию синуса и через функцию косинуса.
  
• 
  Наиболее удобной для расчетов является комплексная фор­ма ряда Фурье.
  

---

Спектры амплитуд и фаз периодических сигналов

Набор гармоник, образующих ряд Фурье (4.10) в тригоно­метрической форме, называют спектром периодического сигна­ла, а наборы амплитуд U_mk и начальных фаз 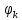этих гармо­ник — спектрами амплитуд и фаз. Каждую гармонику: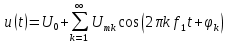

можно отобразить двумя вертикальными линиями. Для этого на одной оси частот необходимо отложить значение частоты этой гармоники 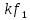и изобразить вертикальную линию высотой, рав­ной амплитуде гармоники 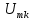затем на другой оси частот на частоте этой же гармоники 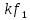изобразить вторую вертикальную линию, равную по высоте начальной фазе гармоники .

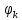Ряд Фурье (4.3) можно переписать в виде



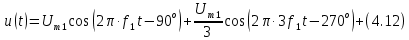
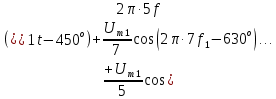
Учитывая, что функция косинуса периодична с периодом 2 = 360°, т.е. ее значения повторяются через 360°, можно вы­честь целое число периодов из фазы гармонических составляю­щих. Тогда получим еще одну форму записи ряда (4.3):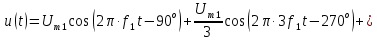
(4.13)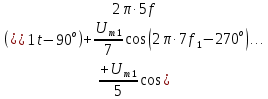


Эти ряды можно изобразить графически. Гармоники этого сигнала, входящие в формулу (4.3), показаны на временных диа­граммах рис. 4.1, б — д. Другой способ графического изображе­ния составляющих ряда Фурье для сигнала на рис. 4.1, а приве­ден на рис. 4.5, а – в. Амплитуды гармоник убывают по закону 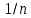, где п — номер гармоники, а фазы гармоник изменяются по закону n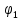

---

где 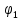— фаза первой гармоники.

Для смещенной на четверть периода периодической последо­вательности прямоугольных импульсов (рис. 4.3, а) формула ря­да Фурье (4.6) может быть видоизменена, если вспомнить, что знак «минус» перед гармоническим колебанием означает поворот колебания по фазе на 180°:


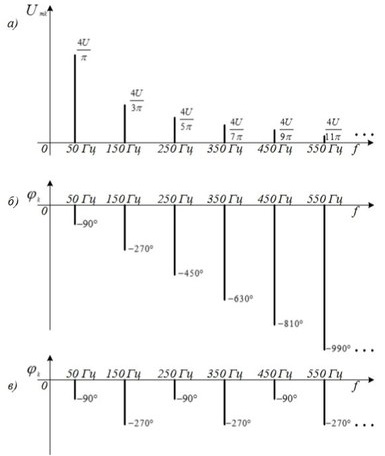
Рис. 4.5. Амплитуды и фазы гармоник сигнала (4.12) и (4.13)




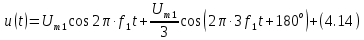
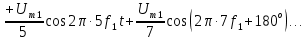
Начальные фазы колебаний в ряде (4.14) поочередно прини­мают значения 0 и 180°. Графическое изображение ряда (4.14) дано на рис. 4.5, а и б.

Вертикальные линии на рис. 4.5 и 4.6 получили название спектральных линий, а наборы этих линий, или, что то же, на­боры амплитуд 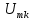и фаз 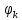гармоник в (4.10), образуют спек­тры амплитуд и фаз данного сигнала.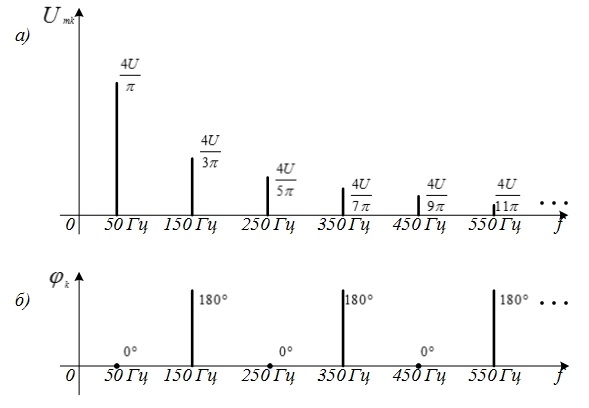


Рис. 4.6. Амплитуды и фазы гармоник сигнала (4.14)

Радиоинженерам знакомы приборы – анализаторы спектров, которые откликаются на каждую гар­монику, входящую в состав сигнала сложной формы и позволяющие их измерять.

Таким образом, спектр амплитуд — это набор амплитуд гармоник 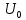, , 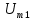, 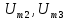... (включая постоянную и ос­новную составляющие), входящих в ряд Фурье, записанный в тригонометрической форме (4.10), а спектр фаз — это набор начальных фаз 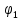, ,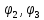 … этих гармоник. Комплексные ам­плитуды 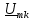из (4.12) образуют комплексный спектр сигнала

---

u(t).

Анализ спектрального (гармонического) состава периодиче­ских сигналов — это вычисление амплитуд 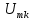и начальных фаз гармонических составляющих ряда Фурье. Обычно для вычисления указанных величин используется форма записи ряда Фурье (4.2):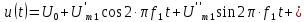




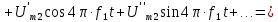
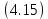
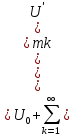
Покажем, что форма записи (4.15) эквивалентна форме запи­си (4.7).

Из приведенных выше рассуждений следует, что для анализа спектрального состава сигнала достаточно знать, как вычислять величины 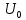, U'_mnи U’_mnв выражении (4.15).

Из формул (4.2) мы знаем, что постоянная составляющая ряда 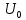вычисляется как среднее значение функции: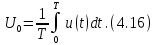


Коэффициенты U'_mk и U''_mk вычисляются как средние взве­шенные значения с весами cosk 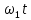и sin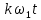 соответственно: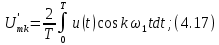


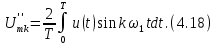
Поскольку, 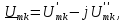то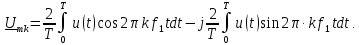

Применяя формулу Эйлера

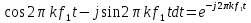
получаем окончательно выражение для комплексного спектра сиг­нала:

---

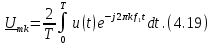
На спектр сигнала влияет не только форма сигнала, но и его параметры. Лучше всего рассмотреть это влияние на кон­кретном примере, а проще всего – на примере периодической последовательности прямоугольных импульсов. В достаточно общем случае эта последовательность изображена на рис. 4.7, а. Пери­од повторения импульсов обозначен Т', а отношение периода к длительности импульсов 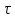' называют скважностьюи обозначают .

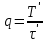Вычисление коэффициентов ряда Фурье в тригонометриче­ской форме по формулам (4.16) — (4.18) приводит нас к записи (см. табл. 4.1)

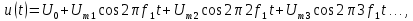
где U₀ = U/q и







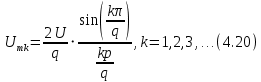
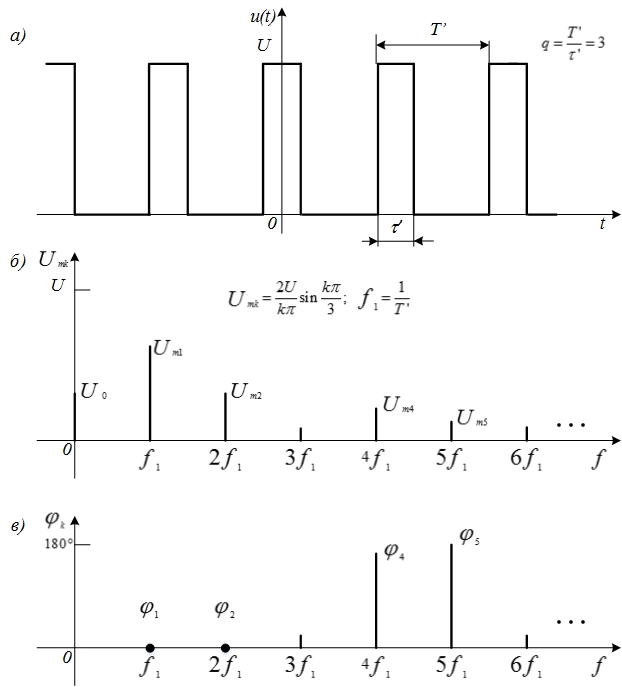
Рис. 4.7. Периодическая последовательность прямоугольных импульсов со скважностью q = 3 и ее спектр

Спектр амплитуд такой периодической последовательности со скважностью q= 3 изображен на рис. 4.7, б.

При значениях k, кратных скважности q импульсной после­довательности, функция 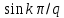принимает нулевые значения и гармоники с этими номерами имеют нулевые амплитуды (в нашем примере с k= 3, 6, 9, ...). Частота первой гармоники определяет­ся по формуле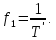

Для гармоник с номерами k, для которых амплитуда 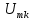по­ложительная, фазовый угол 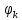равен нулю; для гармоник же с номерами k

---