Файл: Учереждение высшего профессионального образования московский государственный университет приборостроения и информатики.docx

*Функции могут иметь и другой аргумент, например частоту .
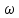Умножение произвольной функции f(t)на sign(t) означает изме­нение знака f(t) в момент времени t = 0.

2. Единичная функция или единичный скачок (функция Хеви­сайда) (табл. 3.1, поз. 2). Функция определяется:
=
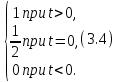
Сопоставляя (3.3) и (3.4), получаем

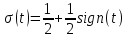
Умножение сигнала s(t) на единичную функцию равносильно включению этого сигнала в момент t = 0
s(t)
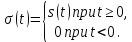
Этим приемом широко пользуются для описания односторонних финитных (ограниченных по времени) сигналов.

3. Дельта-функция или дельта-импульс (функция Дирака) 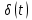(табл. 3.1, поз. 3). По определению -функция удовлетворяет следующим двум условиям:
=
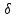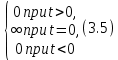
и

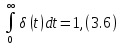
т. е. -функция равна нулю при всех отличных от нуля значениях аргумента

---

, принимая в точке t = 0 бесконечно большое значение. Площадь -функции равна единице.

Остановимся на некоторых свойствах -функции.

а) 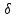(t) является четной функцией аргумента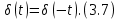

Из (3.6) следует, что

Тогда



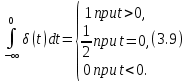
Сопоставляя (3.9) и (3.4), получим

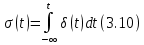
или


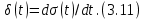
Следовательно, используя понятие δ-функции, можно выразить производную от разрывной функции в точке ее разрыва.

б) фильтрующее свойство δ-функции. Это свойство выражает­ся соотношением

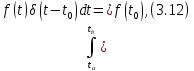
при 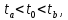т. е. интеграл от произведения произвольной функ­ции f(t), ограниченной в интервале времени ( 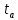, 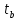), на дельта-функцию 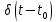равен значению функции f(t) в точке 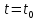(рис. 3.2,а).

в) результатом умножения произвольной функции f(t) на 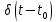является дельта-функция 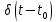, площадь которой равна значению функции f(t) в точке 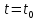(рис. 3.2,б)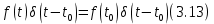

---

г) энергия δ-импульса бесконечно велика. Это легко показать, если воспользоваться одной из моделей дельта-функции – прямо­угольным импульсом длительностью 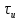с амплитудой 1/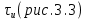


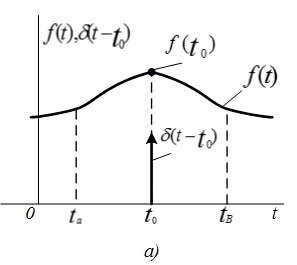
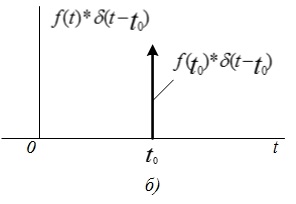
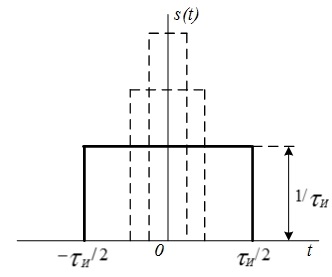
Рис. 3.2. δ-функция (а) и ее фильтрующее свойство (б) Рис. 3.3. Энергия δ-импульса

Энергия такого импульса пропорциональна квадрату его амплиту­ды 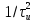и первой степени длительности 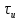(т. е. величине 1/ 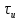). При 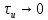, когда прямоугольный импульс превращается в дельта­-функцию, его энергия становится бесконечно большой.

4. Прямоугольный симметричный импульс с единичной высотой Rect (t/ 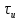) (табл. 3.1, поз. 4), определяемый следующим образом: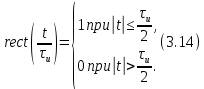

3. 1   ...   4   5   6   7   8   9   10   11   ...   22

---

Методы анализа электрических цепей

Методы, применяемые для расчета реакции цепи на то или иное воздействие, зависят от вида воздействия. В качестве сигнала 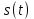в этом случае выступают 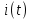– ток, 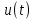– напряжение, 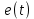– ЭДС. Расчет цепей излагался ранее в разделе «Электротехника» и в [5, 6]. Вспомним и обобщим их результаты.

Если воздействие не зависит от времени, то говорят, что цепь находится в режиме постоянного тока. При этом все индуктивно­сти в цепи представляются, как известно, короткими замыкания­ми (т.е. отрезками проводов), а все емкости – разрывами цепи. Оставшиеся в эквивалентной схеме резистивные сопротивления образуют чисто резистивную цепь. Нахождение напряжений и токов в такой цепи от любых источников не представляет слож­ностей. Методы расчета электрических цепей в режиме постоян­ного тока хорошо описаны в литературе [1, 5, 6]. С математической точки зрения — это методы решения систем линейных алгебраи­ческих уравнений с вещественными коэффициентами. Неизменное во времени воздействие (т.е. постоянный ток или постоянное напряжение) характеризуется только одним парамет­ром – величиной или значением этого воздействия.

Когда же в качестве воздействия рассматривается гармоническое колебание, то необходимо учитывать в общем случае три параметра – его амплитуду, частоту и начальную фазу. Линейная электрическая цепь обладает замечательным свойством: все ее реакции на гар­моническое воздействие будут иметь гармоническую форму и ту же частоту, что и воздействие. Таким образом, линейная элек­трическая цепь не изменяет частоту гармонических колебаний в ней. Кроме того, при наличии в цепи нескольких источников гармонических напряжений и токов одной и той же частоты все реакции цепи будут также гармоническими реакциями той же са­мой частоты.

Следует заметить, что при гармоническом воздействии на ли­нейную электрическую цепь расчет напряжений на элементах и токов в ветвях усложняется. Дело в том, что реактивные элемен­ты (индуктивность и емкость) оказывают влияние не только на

---

амплитуду гармонической реакции, но и изменяют ее начальную фазу. Из трех параметров гармонического колебания (амплитуда, частота и начальная фаза) два подвергаются изменению. Измене­ние амплитуды и начальной фазы гармонического колебания лег­ко отразить в виде изменения длины и положения соответствующего вектора (тока или напряжения) на комплексной плоскости. Действительно, у вектора, как и гармо­нического колебания, может изменяться величина и фазовый угол, отсчитываемый от какой-либо оси.

При заданной частоте гармонических колебаний в цепи воз­действия представляются комплексными числами (или векторами на комплексной плоскости при графическом изображении). Реак­ции цепи будут представляться также комплексными числами, но с другими амплитудами и начальными фазами. Задача анализа цепи – найти эти амплитуды и начальные фазы.

Представление воздействий и реакций в виде комплексных чисел позволяет использовать для расчета (анализа) цепи тот же арсенал методов, который используется для цепей с постоянными воздействиями, с той лишь разницей, что алгебраические опера­ции производятся над комплексными числами. Стандартные ме­тоды расчета линейной цепи сводятся обычно к решению систем линейных алгебраических уравнений с комплексными коэффици­ентами и комплексными переменными. Примеры анализа линей­ных цепей при гармонических воздействиях даны в [1, 5, 6].

При наличии в линейной электрической цепи нескольких ис­точников гармонических колебаний разных частот расчет реакций осуществляется методом наложения. Сначала находится реакция цепи на каждое гармоническое воздействие в отдельности, а затем полученные реакции складываются. Следует только помнить, что сумма гармонических реакций разных частот дает в результате периодическое колебание, которое по своей форме отличается от гармонического.

Тот факт, что периодическое воздействие сложной формы можно представить в виде суммы гармонических колебаний раз­ных частот, лежит в основе расчета цепей с источниками периоди­ческих негармонических сигналов (например, последовательностей прямоугольных, пилообразных, треугольных и тому подобных импульсов). Из математики известно, что представление периоди­ческой функции суммой гармонических колебаний называется разложением этой функции в ряд Фурье.

---