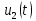Файл: Учереждение высшего профессионального образования московский государственный университет приборостроения и информатики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.04.2024
Просмотров: 406
Скачиваний: 0
СОДЕРЖАНИЕ
Общие сведения об электрических и радиотехнических цепях
Сигналы и их основные характеристики
Корреляционные характеристики детерминированных сигналов
Вопросы и задания для самопроверки:
Методы анализа электрических цепей
Вопросы и задания для самопроверки
Спектры амплитуд и фаз периодических сигналов
Спектральные плотности амплитуд и фаз непериодических сигналов
Примеры определения спектральной плотности сигналов
Определение активной длительности сигнала и активной ширины его спектра
Вопросы и задания для самопроверки:
Комлексная передаточная функция и частотные характеристики цепи
Спектральный анализ цепей при непериодических воздействиях
Вопросы и задания для самопроверки гл. 5, 6:
Вопросы и задания для самопроверки:
Частотный принцип преобразования радиотехнических сигналов
Интегрирование оригинала (теорема интегрирования).
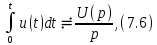
Эта математическая операция показывает, что для нахождения преобразования Лапласа определенного интеграла от оригинала необходимо разделить изображение оригинала на оператор
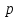 , т.е. операция интегрирования оригинала во временной области заменяется простой операцией деления изображения на
, т.е. операция интегрирования оригинала во временной области заменяется простой операцией деления изображения на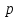 в операторной области.
в операторной области.Данную теорему доказывают, используя свойство дифференцирования оригинала.
Применение теорем дифференцирования и интегрирования оригинала позволяет переходить от интегродифференциальных уравнений для оригинала к более простым алгебраическим уравнениям, записываемым для изображений, и дальнейшему определению оригинала по найденному изображению.
Пример 4. Найдем изображение напряжения, имеющего форму косинусоиды
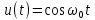 если известно, что напряжение
если известно, что напряжение 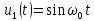 имеет изображение
имеет изображение 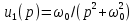 (см. строку 6 в табл. 7.1).
(см. строку 6 в табл. 7.1).Определим производную функции
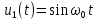
Получим
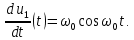
Воспользуемся теоремой дифференцирования (7.5) и получим изображение функции
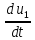 (t):
(t):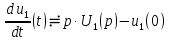
или
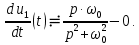
Найдем также изображение функции
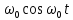 , применив свойство умножения на константу:
, применив свойство умножения на константу:
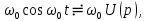
где
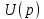 — изображение оригинала
— изображение оригинала 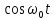 .
.Сравнивая два последних выражения, находим изображение
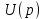 напряжения u
напряжения u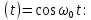

или
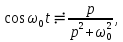
что согласуется со строкой 7 табл. 7.1.
Теорема запаздывания.

Эта математическая запись означает, что сдвиг оригинала
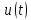 по оси времени на
по оси времени на 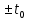 приводит к умножению изображения
приводит к умножению изображения 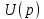 на экспоненту
на экспоненту  .
.Теорема легко доказывается, если осуществить замену переменной
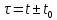 и взять преобразование Лапласа (7.1) функции
и взять преобразование Лапласа (7.1) функции 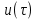 .
.Подобное соотношение можно записать и для оригинала
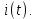 В дальнейшем будем рассматривать свойства преобразований Лапласа главным образом для напряжения
В дальнейшем будем рассматривать свойства преобразований Лапласа главным образом для напряжения 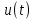 .
.Пример 5. Найдем изображение экспоненциального напряжения (рис. 7.2, а)
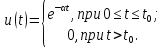
Представим напряжение
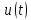 как сумму двух напряжений (рис. 7.2,
как сумму двух напряжений (рис. 7.2,
б):
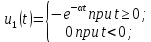

Изображение
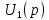 напряжения
напряжения 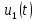 имеет вид (строка 4 табл. 7.1)
имеет вид (строка 4 табл. 7.1)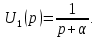
Напряжение
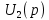 с учетом теоремы запаздывания (7.7) имеет изображение
с учетом теоремы запаздывания (7.7) имеет изображение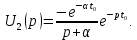
На основании свойства линейности

получаем изображение
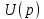 напряжения, показанного на рис. 7.2, а:
напряжения, показанного на рис. 7.2, а:
Этот же результат получается, если найти прямое преобразование Лапласа непосредственно для заданного напряжения:

Имеем
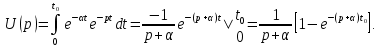
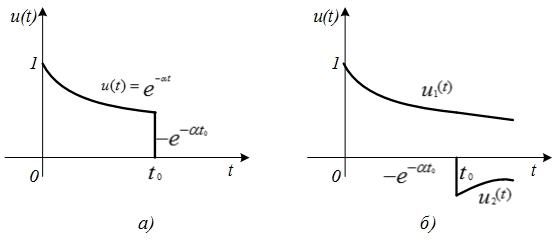
Рис. 7.2. Напряжение в форме экспоненциального импульса
Теорема смещения.

Эта теорема констатирует, что если оригинал
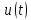 умножается на
умножается на 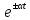 , то изображение этого произведения получается заменой
, то изображение этого произведения получается заменой 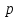 в изображении
в изображении 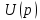 оригинала
оригинала 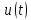 на
на 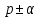 . Причем α может быть как действительной, так и комплексной величиной.
. Причем α может быть как действительной, так и комплексной величиной.
Теорема (7.8) следует непосредственно из прямого преобразования Лапласа, если в (7.1) вместо
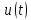 подставить
подставить 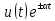 .
.Пример 6. Найдем изображение синусоидального напряжения, амплитуда которого затухает по экспоненциальному закону
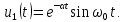
Из табл. 7.1 следует, что оригиналу
 соответствует изображение
соответствует изображение 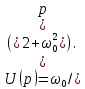 По теореме смещения (7.8) умножение
По теореме смещения (7.8) умножение 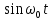 на
на 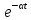 приводит к замене в
приводит к замене в 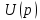 оператора
оператора 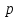 на
на  , поэтому изображение
, поэтому изображение 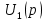 сигнала
сигнала 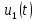 имеет вид
имеет вид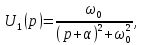
что согласуется со строкой 8 в табл. 7.1.
Теорема подобия (изменение масштаба независимого переменного).

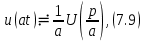
где
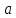 ˗ постоянный вещественный коэффициент. Эта теорема устанавливает, что изменению масштаба оригинала по оси времени соответствует изменение масштаба изображения. Причем умножение времени
˗ постоянный вещественный коэффициент. Эта теорема устанавливает, что изменению масштаба оригинала по оси времени соответствует изменение масштаба изображения. Причем умножение времени 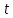 на коэффициента ведет к делению изображения и переменной
на коэффициента ведет к делению изображения и переменной 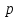 на тот же самый коэффициент
на тот же самый коэффициент 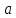 .
.Теорема доказывается следующим образом. Находим прямое преобразование Лапласа (7.1) для оригинала
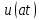 :
:

Пример 7. Найдем изображение
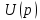 экспоненциального напряжения
экспоненциального напряжения 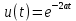 , если известно изображение экспоненциального напряжения
, если известно изображение экспоненциального напряжения 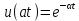
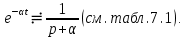
По теореме подобия (7.9) с учетом того, что
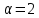 , получаем
, получаем
Пример 8. Найдем теперь изображение
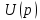 , используя преобразование Лапласа (7.1):
, используя преобразование Лапласа (7.1):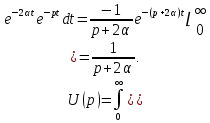
Получили тот же самый результат, что и при применении теоремы подобия.
Теорема свертки.
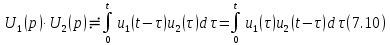
Эта теорема устанавливает, что умножению изображений в области переменной
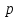 соответствует свертка оригиналов во временной области.
соответствует свертка оригиналов во временной области.Пример 9. Найдем изображение
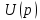 свертки двух напряжений
свертки двух напряжений 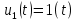 ,
,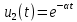 .
.Изображения напряжений
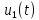 и
и 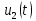 приведены в табл. 7.1:
приведены в табл. 7.1: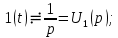
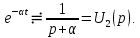
По теореме свертки изображение
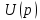 свертки оригиналов имеет вид
свертки оригиналов имеет вид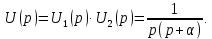
Найдем также изображение свертки оригиналов напряжений
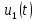 и
и