Файл: Учереждение высшего профессионального образования московский государственный университет приборостроения и информатики.docx

, используя прямое пре­образование Лапласа. Для этого определим вначале функцию свертки:

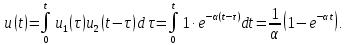
Преобразование Лапласа (7.1) оригинала напря­жения

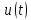
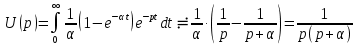
совпадает с изображением, полученным с применени­ем теоремы свертки.

По полученному изображению 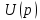легко найти спектр сигнала. Для этого заменяем 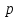на 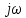и полу­чаем комплексную спектральную плотность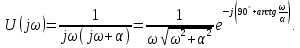

Сопоставление свойств и теорем преобразований Лапласа и Фурье, рассмотренных в гл. 4 и 7, показывает, что при замене опера­тор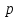а на 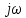и наоборот теоремы и свойства преобразований Лап­ласа и Фурье переходят друг в друга. А это означает, что спектры непериодических сигналов можно вычислить с помощью прямого преобразования Лапласа и его свойств и теорем. В свою очередь, физическая интерпретация теорем спектрального анализа позволяет понять физический смысл теорем операционного исчисления.

Переход от изображений к сигналам. Для нахождения сиг­нала по его изображению можно использовать обратное преобра­зование Лапласа (7.2). Однако обычно такой подход до­вольно трудоемок, и на практике используют более простые спо­собы. Проще всего применить справочные таблицы, устанавли­вающие соответствие между оригиналами и их изображениями для типовых воздействий в электрических цепях, например, мож­но использовать табл. 7.1.

Основные положения изложенных в гл. 7 материалов:

• 
  Преобразование Лапласа является обобщением преобразо­вания Фурье. Заменой оператора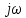 на оператор 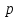и на­оборот осуществляется переход от одного преобразования к другому.
  
• 
  Спектральная плотность сигнала — это сечение его изобра­жения по Лапласу вдоль мнимой оси комплексной плоско­сти. Это означает, что спектры сигналов могут быть вы­числены с помощью прямого преобразования Лапласа и, наоборот, физический смысл теорем операционного исчис­ления раскрывают теоремы о спектрах.
  

---

1. 1   ...   14   15   16   17   18   19   20   21   22

---

Вопросы и задания для самопроверки:

1. 
   Что такое оригинал и изображение сигнала? Как они связаны между собой?
   
2. 
   Какая связь существует между преобразованиями Лапласа и преобразованиями Фурье?
   
3. 
   Найти изображение напряжения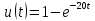 , используя преобразования Лапласа.
   
4. 
   Найти комплексную спектральную плотность напряжения .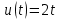
   
5. 
   Какой физический смысл имеют свойства и теоремы преобразований Лапласа?
   

8. Электрические цепи радиотехнических сигналов

Рассматриваются теория и принципы построения цепей радиотехнических устройств: длинные линии, фильтры, модуляторы и демодуляторы, преобразователи и смесители частот.

1. Цепи с распределенными параметрами

8.1.1 Длинные линии и телеграфные сигналы

Цепи, которые рассматривались выше, относятся к классу цепей с сосредоточенными параметрами. Практически все магнитные поля в таких цепях сосредоточены в катушках, все электрические поля ˗ в конденсаторах, а потери ˗ в резисторах.

В цепях с распределенными параметрами потери, емкость и индуктивность распределены в пространстве. В дальнейшем будем рассматривать распределение только вдоль одной пространственной координаты. В этом случае цепи с распределенными параметрами называют длинными линиями.

Простейшим примером цепи с распределенными параметрами может служить двухпроводная линия передачи (рис. 8.1).



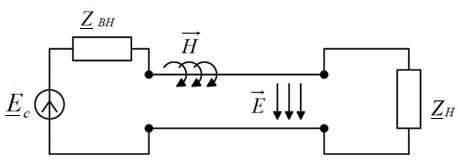
Рис. 8.1. Двухпроводная линия передачи

При протекании тока по проводам вокруг них возникает магнитное поле 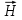, что свиде­тельствует о наличии индуктивности, распределенной вдоль длины линии. Между проводами линии возникает электрическое поле, что говорит о емкости. Провода и диэлектрик между проводами нагреваются, что свидетельствует о наличии распределенных потерь. К цепям с распределенными параметрами относят телефонный провод, коаксиальный кабель, полосковую линию, прямоугольный или круглый волновод, оптоволоконную линию и т. п.

---

Для количественной оценки распределенных параметров используются, следующие погонные параметры длиной линии (параметры единичной длины линии).

1. 
   R₀ ˗ погонное сопротивление потерь в проводниках линии. Определяется как сопротивление проводников короткозамкнутого отрезка линии длиной 1 метр. Единица измерения ˗ Ом/м.
   
2. 
   L₀ ˗ погонная индуктивность. Определяется как индуктивность короткозамкнутого отрезка линии длиной 1 метр. Единица измерения ˗ Гн/м.
   
3. 
   C₀ ˗ погонная емкость. Определяется как емкость между проводами разомкнутого на конце отрезка линии длиной 1 метр. Единица измерения ˗ Ф/м.
   
4. 
   G₀ ˗ погонная проводимость изоляции. Определяется как проводимость между разомкнутыми на конце проводами отрезка линии длиной 1 метр. Единица измерения ˗ См/м.
   

Как правило, численные значения погонных параметров малы. Поэтому распределенные параметры оказывают влияние на передаваемые сигналы только при большой длине линии. На практике эффекты, обусловленные распределенными параметрами, учитывают только тогда, когда длина линии l₀ сравнима или больше длины волны сигнала λ=c/f, где с ˗ скорость света, f ˗ частота.

Рассмотрим установившиеся напряжение 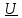и ток 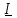в произвольном сечении длинной линии на расстоянии l от нагрузки (рис. 8.2,а). Выделим отрезок с малой длиной Δl, примыкающий к рассматриваемому сечению. Так как величина Δl<<λ, то отрезок можно представить в виде четырехполюсника с сосредоточенными параметрами (рис. 8.2,б). На выходных зажимах отрезка из-за влияния распределенных параметров ток и напряжение уменьшаются на Δt и ΔÚ соответственно.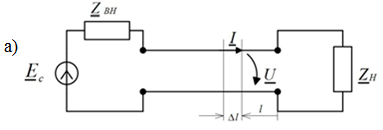




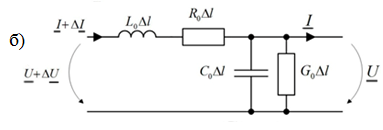
Рис 8.2. Изображение сечения длинной линии (а) и его эквивалентная схема замещения (б)

Из анализа цепи (рис. 8.2, б) следует, что изменение напряжения 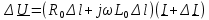. Раскрывая круглые скобки и пренебре­гая величинами второго порядка малости, получим следующее выра­жение: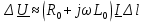

---

. Разделив правую и левую части равенства на Δl и переходя к пределу 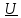при 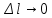, получим первое телеграфное уравнение длинной линии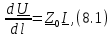

где 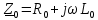˗ погонное комплексное сопротивление. Из этого уравнения следует, что комплексная амплитуда напряжения вдоль линии будет обязательно изменяться, если в сечении линии имеется не равный нулю ток (производная в (8.1) не равна нулю).

Используя первый закон Кирхгофа для выходного узла отрезка длинной линии (рис. 8.2, б), получим 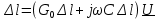. Разделив правую и левую части равенства на 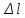и переходя к пределу при 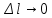, получим второе телеграфное уравнение длинной линии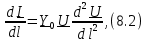

где 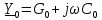˗ погонная комплексная проводимость длинной линии. Из второго телеграфного уравнения следует, что при наличии напряжения в линии комплексная амплитуда тока вдоль линии будет изменяться. Телеграфные уравнения были получены в конце XIX века при исследовании линий телеграфной связи.

Дифференцируя уравнение (8.1) и подставляя в это уравнение вме­сто производной от тока правую часть уравнения (8.2), получим одно­родное линейное дифференциальное уравнение относительно напря­жения в произвольном сечении линии:




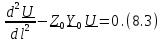
Из теории, дифференциальных уравнений известно, что решение уравнения (8.3) записывается в виде

---