Файл: Учереждение высшего профессионального образования московский государственный университет приборостроения и информатики.docx

похожи на процессы в линии, т. е. цепь представляет собой как бы искусственную длинную линию. Если такую «линию» согласовать с нагрузкой, то ее, очевидно, можно использовать для задержки сигналов.



Рис. 8.9. Эквивалентная схема отрезка длинной линии

Конечно, указанная аналогия имеет формальный характер. На самом деле рассматриваемая цепь не является системой с распределенными параметрами, и, стало быть, волновые процессы в ней существовать не могут. Запаздывание выходного сигнала относительно входного в данном случае есть лишь следствие возникающих в цепи переходных явлений.

Перейдем к анализу процессов в схеме, изображенной на рис. 8.8. Для этого представим ее в виде последовательной цепочки 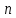идентичных симметричных четырехполюсников, работающих в согласованном режиме (рис. 8.10)



Рис. 8.10. Последовательная цепочка симметричных идентичных четырехполюсников.

Комплексную амплитуду напряжения на входе системы обозначим 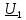а на выходе — 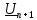. Тогда отношение этих амплитуд будет равно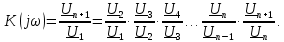

Так как для p-го четырехполюсника

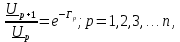
где Г_р — коэффициент распространения, то


.

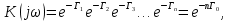
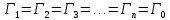Постоянная 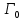для Т-образной ячейки фильтра нижних частот определяется известным выражением: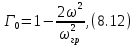



где .

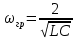Из этого выражения, видно, что в полосе прозрачности, т. е. при 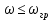постоянная 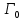есть мнимая величина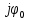

---

. Следовательно, на интервале 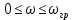модуль передаточной функции цепи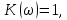

а фазо-частотная характеристика

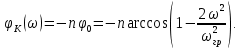
Последняя на начальном участке (см. рис. 8.11) достаточно близка к прямой линии.



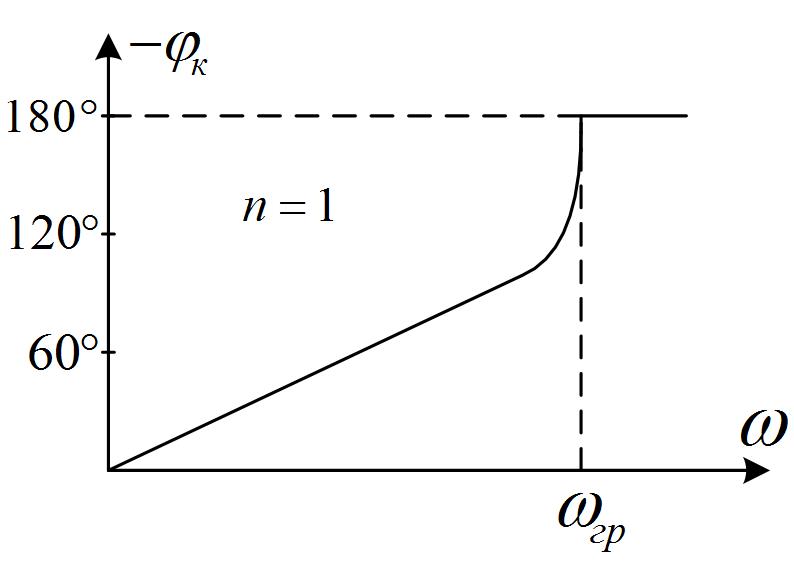
Рис. 8.11. Фазовая характеристика фильтра нижних частот.

Вычислим время задержки 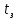, полагая, что ширина спектра сигнала значительно меньше полосы прозрачности. Для этого входное напряжение 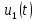и выходное 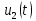представим в виде: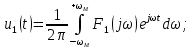






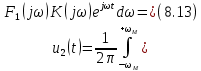
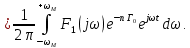
Здесь 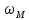максимальная частота спектра сигнала, причем 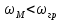. Разложим функцию 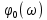в окрестности точки 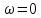в степенной ряд .

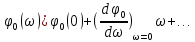Так как по условию 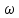мало и 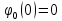, приближенно можно полагать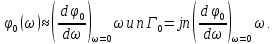

Подставляя последнее выражение в равенство (8.13), находим
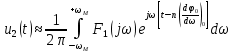(8.14)
Нетрудно заметить, что правая часть в последнем соотношении фактически представляет собой напряжение на выходе фильтра нижних частот с равномерной в пределах полосы 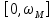амплитудной частотной характеристикой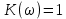

---

и линейной фазовой характеристикой

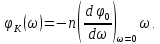
Применяя к соотношению (8.14) теорему запаздывания, получим


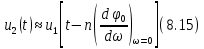
Из выражения (8.15) следует, что время задержки сигнала


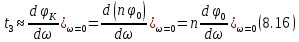
Для цепи, изображенной на рис. 8.8, а,

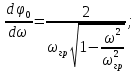
при ω = 0

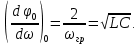
Следовательно,

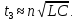
Полученное выражение дает вполне удовлетворительный результат, если 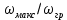превышает 0,5, т. е.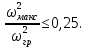

Характеристическое сопротивление фильтра

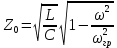
в этом случае приближенно можно считать постоянным:



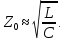
Таким образом, реальная цепь может быть использована для задержки управляющих (низкочастотных) колебаний, если ее частотные характеристики, по крайней мере, в пределах ширины спектра сигнала, близки к характеристикам идеального фильтра с П-образной амплитудно-частотной и линейной фазо-частотной характеристиками. Только в этом случае сигнал будет проходить по цепи, не испытывая заметных искажений.

Сравним в заключение выражения (8.11) и (8.16), характеризующие время задержки .

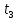Совершенно ясно, что величина 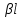в задерживающей цепи с распределенными параметрами и величина 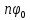в многозвенном фильтре имеют одинаковый смысл: обе они определяют фазовый сдвиг между колебаниями на входе и выходе системы. Если этот сдвиг в обоих случаях обозначить буквой 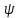, то формулы (8.11), (8.16) можно записать в виде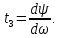

Следовательно, время задержки сигнала в цепи с сосредоточенными параметрами мы можем формально определить как время «пробега» сигнала по цепи.

Основные положения изложенных в п. 8.1 материалов:

---

• 
  Напряжения (первое телеграфное уравнение) и ток (второе телеграфное уравнение) меняются вдоль линии связи (проводная, коаксиальная, шинная и т.д.);
  
• 
  Бегущая падающая электромагнитная волна обеспечивает наибольшую энергию передаваемого сигнала, бегущая отраженная волна- подавляет сигнал;
  
• 
  Баибольшая эффективность передачи сигнала обеспечивается в режиме согласования сопротивлений линии передачи и нагрузки;
  
• 
  Задержку сигнала во времени обеспечивают специальные схемы собранные из дискретных R, L и C элементов- линии задержки;
  
• 
  Время задержки сигнала в цепи определяется ее параметрами и соответствуют фазовому сдвигу колебаний на ее входе и выходе;
  

2. 1   ...   14   15   16   17   18   19   20   21   22

---

Частотный принцип преобразования радиотехнических сигналов

8.2.1 Модулированные сигналы и их спектры

В устройствах связи и в компьютерных сетях широко используется частотный принципразделения сигналов. В соответствии с этим принципом сигналам отводятся неперекрывающиеся узкие полосы частот из всего диапазона частот, занимаемого системой передачи информации. С помощью узкополосных сигналов легко организовать передачу информации от большого числа источников к большому числу получателей, при этом источники не будут мешать друг другу.

Кроме частотного принципа в связи используется временной прин­ципразделения сигналов, когда каждому сигналу отводится неболь­шой промежуток времени из некоторого большого повторяющегося временного интервала, отведенного множеству сообщений. Времен­ной принцип часто используется в телефонии.

Частотный принцип разделения сигналов используется в радио- и телевещании, в устройствах мобильной связи, при передаче информа­ции с помощью модемов и т. п. Большинство узкополосных сигналов, располагаясь в области высоких частот системы связи, являются вы­сокочастотными колебаниями. Важное преимущество высокочастотных сигналов состоит в том, что они хорошо излучаются неболь­шими по размеру антенными устройствами и могут распространяться на большие расстояния.

Речевые и музыкальные сигналы, видеосигналы, сигналы, содер­жащие цифровую информацию и т. п., являются относительно низ­кочастотными сигналами. Их спектр занимает диапазон частот, начинающийся вблизи нуля и заканчивающийся некоторой верхней частотой. Например, телефонный речевой сигнал занимает диапазон частот от 300 Гц до 3400 Гц.

Проблема передачи информации, содержащейся во многих низко­частотных сигналах, с помощью множества узкополосных каналов связи с разными частотами решается при использовании модулиро­ванных сигналов. Модулированный сигнал— это узкополосный сиг­нал, параметры которого изменяются пропорционально низкочастот­ному информационному сигналу. Как правило, модулированный сигнал является высокочастотным колебанием. Для получения моду­лированного сигнала используется гармонический сигнал 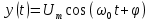, называемый в этом случае несущим колебанием (несущей частотой)

---