Файл: Учереждение высшего профессионального образования московский государственный университет приборостроения и информатики.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 10.04.2024
Просмотров: 402
Скачиваний: 0
СОДЕРЖАНИЕ
Общие сведения об электрических и радиотехнических цепях
Сигналы и их основные характеристики
Корреляционные характеристики детерминированных сигналов
Вопросы и задания для самопроверки:
Методы анализа электрических цепей
Вопросы и задания для самопроверки
Спектры амплитуд и фаз периодических сигналов
Спектральные плотности амплитуд и фаз непериодических сигналов
Примеры определения спектральной плотности сигналов
Определение активной длительности сигнала и активной ширины его спектра
Вопросы и задания для самопроверки:
Комлексная передаточная функция и частотные характеристики цепи
Спектральный анализ цепей при непериодических воздействиях
Вопросы и задания для самопроверки гл. 5, 6:
Вопросы и задания для самопроверки:
Частотный принцип преобразования радиотехнических сигналов
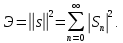
Физический смысл полученного выражения для пространства L2 следующий: энергия сигнала равна сумме энергий всех компонент, из которых складывается обобщенный ряд Фурье.
Это значит для разных форм представления сигнала
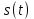 :
: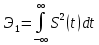 - в виде временной функции (см п. 2.1);
- в виде временной функции (см п. 2.1);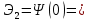 в виде корреляционной функции (см п. 2.2);
в виде корреляционной функции (см п. 2.2);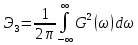 в виде спектральной функции (см п. 4.5),
в виде спектральной функции (см п. 4.5),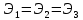 .
.Если использовать в качестве ортогональных базисных функций 1,
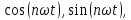 где n = 1, 2, ….то получим ряд Фурье. Ряд Фурье используется, если сигнал s(t)
где n = 1, 2, ….то получим ряд Фурье. Ряд Фурье используется, если сигнал s(t)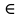 L2(T) представлен на ограниченном временном отрезке [0, T], либо сигнал является периодическим с периодом Т. Ряд Фурье записывается в разных формах: тригонометрической, комплексной, интегральной (см. Глава 4 настоящей работы). Также в качестве базисных функций используют: функции Лежандра; Чебышева, Эрмита и Лагерра; на основе которых осуществляется разложение непрерывной функции
L2(T) представлен на ограниченном временном отрезке [0, T], либо сигнал является периодическим с периодом Т. Ряд Фурье записывается в разных формах: тригонометрической, комплексной, интегральной (см. Глава 4 настоящей работы). Также в качестве базисных функций используют: функции Лежандра; Чебышева, Эрмита и Лагерра; на основе которых осуществляется разложение непрерывной функции
f(x) в обобщенные ряды Фурье [1, 2]. При проведении теоретических исследований и при решении задач удобно использовать преобразование Лапласа (см. п. 7 настоящей работы). Это преобразование вводится для всех сигналов s(t), тождественно равных нулю при t < 0 и возрастающих не быстрее
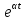 где
где 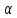 — вещественное число, причем
— вещественное число, причем 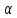 > 0.
> 0.Преобразование Лапласа можно получить как обобщение преобразования Фурье, обозначая
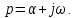
Для анализа cигналов
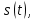 заданных на всей временной оси
заданных на всей временной оси 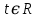 , в настоящее время часто используются негармонические базисные функции вейвлеты (wavelet) [2]. Название "вейвлет", переводится на русский язык как "маленькая волна". Вейвлет представляется функцией
, в настоящее время часто используются негармонические базисные функции вейвлеты (wavelet) [2]. Название "вейвлет", переводится на русский язык как "маленькая волна". Вейвлет представляется функцией 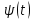 осциллирующей в некотором временном интервале подобно волне и быстро затухающей вне него. При этом функция
осциллирующей в некотором временном интервале подобно волне и быстро затухающей вне него. При этом функция 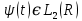 должна иметь нулевое среднее значение
должна иметь нулевое среднее значение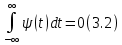
Н
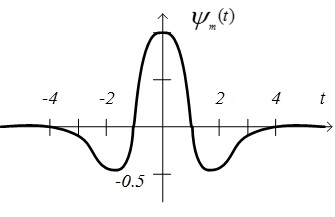
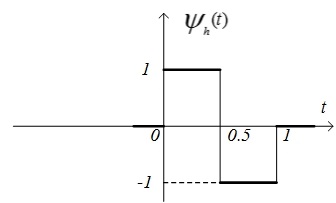
а рис. 3.1 показаны графики двух вейвлетов: мексиканская шляпа
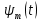 и Хаара
и Хаара 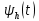 .
.а) б)
Рис. 3.1. Графическое изображение вейвлетов: а) – мексиканская шляпа, б) - Хаара
Общий принцип построения базиса на основе вейвлета состоит в использовании масштабирования (сжатия или растяжения) базисной функции во времени и сдвига (смещения) ее по временной оси. Таким образом, вейвлеты — это функции
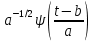 , где: а – масштаб, b – сдвиг. Коэффициент
, где: а – масштаб, b – сдвиг. Коэффициент 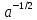 перед функцией
перед функцией 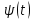 введен для сохранения нормы сигнала
введен для сохранения нормы сигнала 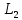 (R).
(R).Чем больше масштаб
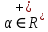 , тем медленнее изменяется и более «крупномасштабно» выглядит вейвлет. Чем меньше
, тем медленнее изменяется и более «крупномасштабно» выглядит вейвлет. Чем меньше 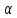 , тем более высокочастотные и быстроизменяющиеся составляющие описывает вейвлет. Понятие частоты из классического гармонического спектрального анализа в вейвлет-анализе заменено масштабом
, тем более высокочастотные и быстроизменяющиеся составляющие описывает вейвлет. Понятие частоты из классического гармонического спектрального анализа в вейвлет-анализе заменено масштабом 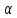 .
.Используя сдвиг
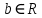 вейвлета по оси времени, проводим анализ свойств сигнала в разных точках временной оси. Такой сдвиг не предусмотрен в гармоническом анализе. Поэтому вейвлеты удобно использовать при анализе нестационарных сигналов, когда кроме информации о выявленных частотах нужно получить данные о моментах времени, при которых эти частоты возникают или исчезают.
вейвлета по оси времени, проводим анализ свойств сигнала в разных точках временной оси. Такой сдвиг не предусмотрен в гармоническом анализе. Поэтому вейвлеты удобно использовать при анализе нестационарных сигналов, когда кроме информации о выявленных частотах нужно получить данные о моментах времени, при которых эти частоты возникают или исчезают.Подобно тому как аналоговые воздействия были представлены преобразованиями Фурье и Лапласа, дискретные воздействия представляются Z-преобразованием [1, 2]. Дискретные цепи описываются во временной области разностными уравнениями, а на комплексной плоскости — передаточной функцией комплексного переменного
Z. Расчет реакции дискретной цепи на дискретное воздействие может быть осуществлен как временным методом, так и с помощью передаточных функций и Z-преобразования. Методы анализа дискретных цепей описаны в [1, 2, 3].
- 1 2 3 4 5 6 7 8 9 10 ... 22
Простейшие разрывные функции
Для расчета характеристик электрических цепей во временной области используются испытательные сигналы. Простейшие разрывные функции, которыми широко пользуются в теории сигналов, моделировании и испытании цепей, представлены в табл. 3.1. Ниже приводится краткое описание этих функций.
1. Функция знака
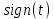 (сигнум-функция) (табл. 3.1, поз 1). Функция имеет постоянную величину, равную единице, знак которой скачком изменяется при переходе переменной t через нуль
(сигнум-функция) (табл. 3.1, поз 1). Функция имеет постоянную величину, равную единице, знак которой скачком изменяется при переходе переменной t через нуль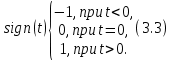
Таблица 3.1
| № п/п | Название функции* | Аналитическая запись функции | Графическое изображение | Связь между функциями |
| 1 | Функция знака sign(t) (сигнум- функция) | Sign(t)= 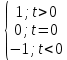 | 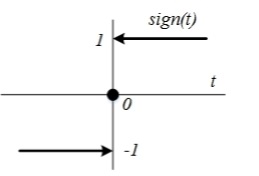 | _ |
| 2 | Единичная функция (функция Хевисайда)  | 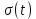 = =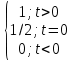 | 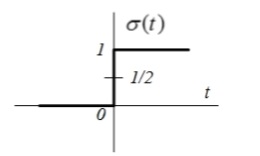 | 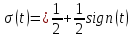 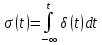 |
| 3 | Дельта-функция (функция Дирака) 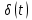 | 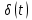 = =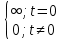 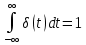 | 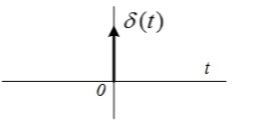 | 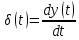 |
| 4 | Прямоугольный импульс с единичной высотой rect(t/ 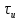 ) ) | 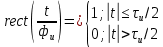 | 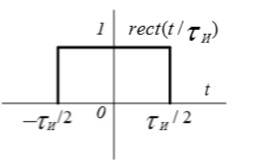 | 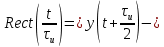 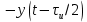 |


