Файл: прикладная математика учебное пособие московский автомобильнодорожный.docx

программирования. Любую другую задачу математического програм- мирования, не удовлетворяющую условиям (1.3) и (1.4), условимся считать нелинейной.

Класс задач нелинейного программирования значительно шире класса задач линейного программирования. Основные результаты в нелинейном программировании получены при рассмотрении задач, в которых система ограничений (1.1) линейная, а целевая функция не- линейная. Даже в таких задачах решение может быть найдено только для узкого класса целевых функций. Еще большие трудности возни- кают при решении задач с нелинейными ограничениями. Здесь найти оптимальное решение возможно при условии, что целевая функция и функции, образующие систему ограничений, удовлетворяют подхо- дящим свойствам.

Рассмотрим примеры решения задач нелинейного программиро- вания. Так же как и в линейном программировании, они могут быть решены графически.

В евклидовом пространстве E_n

система ограничений (1.1) опре-

деляет область допустимых решений задачи. В отличие от задачи ли- нейного программирования она не всегда является выпуклой. Если определена область допустимых решений, то нахождение решения задачи (1.1, 1.2) сводится к определению такой точки этой области, через которую проходит гиперповерхность наивысшего (для задачи на поиск максимального значения целевой функции) или наинизшего

(поиск минимального значения) уровня

f(x₁, x₂,..., x_n)  h.

Указанная

точка может находиться как на границе области допустимых решений, так и внутри нее. Процесс нахождения решения задачи нелинейного программирования (1.1, 1.2) с использованием ее геометрической ин- терпретации включает в себя следующее:

находят область допустимых решений задачи, определяемую со- отношениями (1.1) (если она пуста, то задача не имеет решения);
строят гиперповерхность f(x₁, x₂,..., x_n)  h;
определяют гиперповерхность наивысшего (наинизшего) уровня или устанавливают неразрешимость задачи из-за неограничен- ности функции (1.2) сверху (снизу) на множестве допустимых решений;
находят точку области допустимых решений, через которую про- ходит гиперповерхность наивысшего (наинизшего) уровня, и оп- ределяют в ней значение функции (1.2).

Примеры решения задач нелинейного программирования

Пример 1. Найти минимальное и максимальное значения функ-

ции Z=(x 4)²  (x 6)² при ограничениях:

1 2

_^x¹^^x²^^1,

_2x₁ 3x₂ 12,

^_x₁ 0, x₂ 0.

Решение. Область допустимых решений представляет собой многоугольник ABCD (рис. 1.1).

Прямая ABзадается уравнением

2x₁ 3x₂

 12,

а прямая CD–

уравнением

x₁ x₂ 1.

Если положить Z=Q(Q> 0), то получается (x 4)²  (x 6)² =Q

1 2

– уравнение окружности с центром в точке М(4; 6). С уменьшением

(увеличением) Q (квадрата радиуса) значение Z соответственно уменьшается (увеличивается).

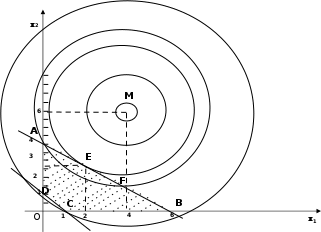
Рис.1.1.Нелинейнаязадача,окружность

Расстояния от точки Мдо точек А(0; 4), B(6; 0), С(1; 0), D(0; 1)

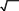
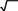равны соответственно МА = 2 5, МВ = 2 10, МC = 3 5, МD = 41. Окружность радиуса МА (наименьшего из них) пересекает прямую ABв точке F (48/13; 20/13), находящейся внутри отрезка AB, являющуюся как и точка А(0;4) решением системы уравнений:

^(x 4)²  (x

 6)²  20,

^1  3x 2

_2x_{1 2}12.

Следовательно, радиус окружности можно еще уменьшить, а ми- ^{нимальное значение функции}^Z^{будет меньше}^МА⁼2 5. ^{Очевидно}^,что минимальное значение равное МЕ = 196/13 функция Z принимает в точке Е(24/13; 36/13), в которой окружность касается области реше- ний. Точка Ене является вершиной многоугольника ABCD, а ее коор- динаты находятся в результате решения системы уравнений, соответ- ствующих пересечению прямых ME и АВ, касающихся окружности в точке Е:

³^x¹^²^x²^^0,

^2x 3x 12.

 1 2

Уравнение прямой ME находится так. Прямая ME перпендикуляр- на AB (так как радиус окружности, проведенный в точку касания, пер- пендикулярен самой касательной) и проходит через точку M, т.е. уравнение прямой ME: 3(x₁ 4)  2(x₂ 6)  0.

Окружность радиуса МС(наибольшего из них) пересекает оси

Ox₁

и Ox₂

в точках, не принадлежащих отрезкам ADи BСсоответст-

венно, а значит и многоугольнику ABCD. Поэтому величина квадрата радиуса МСсоответствует наибольшему значению функции Z= 45.

Итак, вершина C – точка глобального максимума, а E – точка гло- бального минимума.

Пример 2. Найти минимальное и максимальное значения функ-

2 1 1
ции Z=x

 x²  8x

при ограничениях:

³^x¹^^x²^^18,

⁹^x₁^²^x₂^^45,

^x 2x 2,

_1 2

 0,

 0.

^^x1 ^x2

Решение. Область допустимых решений представляет собой многоугольник ABCDE (рис. 1.2).

Прямая ABзадается уравнением

3x₁  x₂  18,

прямая CВ–

9x₁  2x₂  45,

а прямая DE–

x₁ 2x₂ 2.

Следовательно, для нахож-

дения минимального и максимального значения функции Zдостаточ- но определить нужные точки многоугольника ABCDE. Очевидно, что искомые точки находятся на его границе, но не обязательно являются вершинами многоугольника ABCDE.

2 1 1
Если положить Z=Q(Q> 0), то получается x

 x²  8x

=Q–

уравнение параболы с вершиной в точке, абсцисса которой равна 4. С уменьшением (увеличением) Q график параболы сдвигается вниз (вверх), а значение функции Zуменьшается (увеличивается).

Координаты точки B (3; 9) – пересечения прямых AB и BC много- угольника ABCDEнаходятся как решение системы уравнений:

³^x¹^^x²^^18,

^9x 2x 45.

 1 2

Смотрите также файлы

Протокол от 31. 05. 22г. Т. А. Сажина Согласовано заместителем директора по увр.. 2022 г.docx

2. финансовый анализ на примере коммерческого банка паосбербанк 1 организационная характеристика пао сбербанк.docx

Слайд бихевиоризм (от англ behavior поведение) направление в американской психологии, утвердившее ее предметом поведение, понимаемое как совокупность объективных реакций на внешние стимулы и не требующее для своего объяснения обращения к психическим явлен.docx

Угольный фильтр Ионообменный фильтр.docx

Реабилитация пациентов с острой и хронической цереброваскулярной недостаточностью.docx

Файл: прикладная математика учебное пособие московский автомобильнодорожный.docx

Примеры решения задач нелинейного программирования

Смотрите также файлы

Информация

Списки файлов

Дополнительно