Файл: прикладная математика учебное пособие московский автомобильнодорожный.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.02.2024
Просмотров: 180
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Задачи выпуклого программирования
Решение задачи нелинейного программирования в Excel
Задания к самостоятельной работе
К ЗАДАЧАМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задания для самостоятельного решения
КООПЕРАТИВНЫЕ ИГРЫ И ДРУГИЕ ЗАДАЧИ
Параметры сетей и методы их расчета
Матричный метод расчета сетевого графика
Табличный метод расчета сетевого графика
Таблица стандартного нормального распределения
Анализ и оптимизация сетевой модели
Управление производством работ по сетевым графикам
Проект СРМ и временной резерв стадий
Проект СРМ и временной резерв стадий
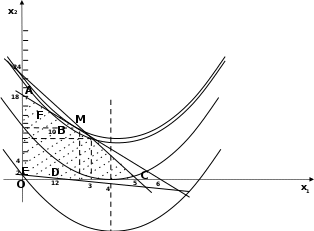
Рис.1.2.Нелинейнаязадача,парабола
Остальные точки многоугольника ABCDE имеют координаты:
А(0; 18), C(5; 0), D(2; 0), Е(0; 2).
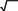 Парабола, проходящая через точку Е(0; 2), пересекает ось
Парабола, проходящая через точку Е(0; 2), пересекает осьOx1 в
точках с абсциссами равными 4
14,
являющимися решениями
уравнения
x2 8x 2
(Q= 2), не принадлежащих отрезку DС
1 1
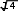
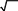 (4 2 5 4 14 ), а значит, и многоугольнику ABCDЕ. Поэтому
(4 2 5 4 14 ), а значит, и многоугольнику ABCDЕ. Поэтому величина Q= 2 соответствует наименьшему значению функции Z= 2.
Парабола, проходящая через точку В(3; 9) прямую ABв точке F (2; 12), находящейся внутри отрезка AB, являющейся как и точка Врешением системы уравнений при Q= 9 32 8 3 24:
3x1 x2 18,
x
2 1 1
x2 8x 24.
Следовательно, график параболы можно еще поднять вверх, а максимальное значение функции Z будет больше 24. Очевидно, что максимальное значение функция Z принимает в точке М, в которой график параболы касается области решений. Точка Мне является
вершиной многоугольника ABCD, а ее координаты находятся из сле- дующих соображений. Прямая АВ касается графика параболы в точке М, следовательно, в этой точке совпадают значения их производных
x2' 2x1 8
и x2' 3:
2x1 8 3,
x
3
x 18,
x
1 2
2 1 1
x2 8x
Q.
Решением этой системы будут координаты точки М(5/2; 21/2) и значение Q = 97/4, соответствующее наибольшему значению функции Z= 24,25.
Итак, вершина М– точка глобального максимума, а E–точка гло- бального минимума.
Пример 3. Найти минимальное и максимальное значения функ-
ции Z=
2x2 x1 x2 2x1 при ограничениях:
x1 2x2 12,
3x2 x1 8,
2x 9x 29,
1 2
x1 0, x2 0.
Решение. Область допустимых решений представляет собой треугольник ABC (рис. 1.3). Прямая AB задается уравнением
3x2 x1 8,
прямая CВ–
x1 2x2 12,
а прямая АС–
2x1 9x2 29.
Следовательно, для нахождения минимального и максимального зна- чения функции Zдостаточно определить нужные точки треугольника ABC. Очевидно, что искомые точки находятся на его границе, но не обязательно являются вершинами треугольника ABC.
Если положить Z=Q(Q> 0), то получается (x2 1)(2x1 1)
=Q+ 1
– уравнение гиперболы с асимптотами
x2 1 и
x1 0,5.
С умень-
шением (увеличением) Qграфик гиперболы выгибается вниз (вверх),
а значение функции Zуменьшается (увеличивается).
Координаты точки B(4; 4) – пересечения прямых BCи ABтре- угольника ABCнаходятся как решение системы уравнений:
x1 2x2 12,
3x x 8.
2 1
Остальные точки треугольника ABCнаходятся аналогично.
Координаты точки А(1; 3) – пересечения прямых АCи ABтре- угольника ABCнаходятся как решение системы уравнений:
2x1
9x2 29,
3x x 8.
2 1
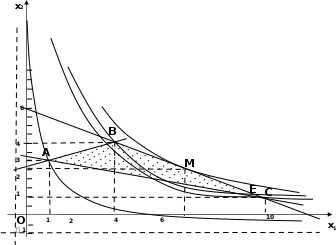
Рис.1.3.Нелинейнаязадача,гипербола
Координаты точки С(10; 1) – пересечения прямых BCи AСтре- угольника ABCнаходятся как решение системы уравнений:
x1 2x2 12,
2x 9x 29.
1 2
График гиперболы при Q=
2x2 x1 x2 2x1 2 3 1 3 2 1 11
проходит через точку А(1; 3), а при Q=
2x2 x1 x2 2x1 2 110
1 2 10 41 проходит через точку С(10; 1). Поэтому величина Q=
= 11 соответствует наименьшему значению функции Z= 11.
График гиперболы при Q=
2x2 x1 x2 2x1 2 4 4 4 2 4 44
проходит через точку В(4; 4) и пересекает отрезок BC, в точке Е(9,5; 1,25), находящейся внутри отрезка BC, являющейся как и точка Врешением системы уравнений
x1 2x2 12,
2xx x 2x
44.
2 1 2 1
Решением квадратного уравнения
2x2 (12 2x2 ) x2 2(12 2x2 ) 44,
получающегося подстановкой значения первого уравнения системы
во второе, являются значения
x2 4
(соответствует точке В) и
x2 1,25
(соответствует точке Е).
Следовательно, график гиперболы можно еще выгнуть вверх, а максимальное значение функции Z будет больше 44. Очевидно, что максимальное значение функция Z принимает в точке М, в которой график гиперболы касается области решений. Точка М не является вершиной треугольника ABC, а ее координаты находятся из следую- щих соображений. Прямая СВ касается графика гиперболы в точке М, следовательно, в этой точке совпадают значения их производных
2 2
x' 0,5
и x'
2Q 2 :
 (2x1
(2x1 1)2
2Q 2
1 ,

 (2x
(2x 1)2 2
x 1
12,
1 2x2
2x2 x1 x2 2x1 Q,
Q 825 ,



