Файл: прикладная математика учебное пособие московский автомобильнодорожный.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.02.2024
Просмотров: 173
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Задачи выпуклого программирования
Решение задачи нелинейного программирования в Excel
Задания к самостоятельной работе
К ЗАДАЧАМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задания для самостоятельного решения
КООПЕРАТИВНЫЕ ИГРЫ И ДРУГИЕ ЗАДАЧИ
Параметры сетей и методы их расчета
Матричный метод расчета сетевого графика
Табличный метод расчета сетевого графика
Таблица стандартного нормального распределения
Анализ и оптимизация сетевой модели
Управление производством работ по сетевым графикам
Проект СРМ и временной резерв стадий
Проект СРМ и временной резерв стадий
v
0,375,
1
v
0,625,
2
a/ v a/ v 5,375.
11 1 12 2
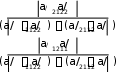
u
0,875,
1
u
0,125,
4
a/ u a/ u
5,375.
11 1 11 4
1 4
Следовательно, оптимальная стратегия из системы уравнений.
u (u,0,0,u )
находится
Итак, решением игры являются следующие смешанные стратегии
v (0,375;0,625)
1 ... 12 13 14 15 16 17 18 19 ... 42
5,375.
и u (0,875;0;0;0,125)
с ценой игры равной
- Пример решения игры, заданной матрицей 33
Пример 4. Автомобильный завод планирует выпускать в текущем году с конвейера три модели автомобилей А, Б и В. Рассматриваются три варианта развития экономической ситуации в стране. Причем ка- ждый из этих вариантов потребует своих затрат и обеспечивает раз- личный экономический эффект. Прибыль (млн. руб.), которую получа- ет завод при данном объеме выпуска соответствующей модели и со- стояния спроса на нее, определяется табл. 2.1.
Таблица2.1
Модели и варианты
| Модели | Варианты | ||
| I | II | III | |
| А | 110 | 120 | 115 |
| Б | 150 | 160 | 120 |
| В | 125 | 105 | 110 |
Требуется определить объем выпуска моделей автомобилей, обес- печивающий среднюю величину прибыли, при любом состоянии спроса.
Решение. 1. Проверим матрицу на наличие седловой точки:
max(minaij) 120, min(max aij) 120.
1i3
1 j3
1 j3 1i3
Так как
,
то игра имеет Седловую точку, соответствующую
III варианту выпуска модели Б. Объем выпуска соответствующей мо- дели обеспечивает прибыль 120 млн. руб. при любом варианте разви- тия экономической ситуации в стране.
- 1 ... 13 14 15 16 17 18 19 20 ... 42
СВЕДЕНИЕ ЗАДАЧИ ТЕОРИИ ИГР
К ЗАДАЧАМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
-
Постановка задачи
Рассмотрим платежную матрицу (матрицу игры) размерностью
k n,
где
k,n 2:
a11 a12 ... a1n
a a ... a
A
21 22 2n.
... ... ... ...
a a ... a
k1 k2 kn
Тогда, согласно вышеприведенной теории, у каждого игрока сущест-
вуют свои оптимальные стратегии u (u,u,...,u ) и v (v,v,...,v ). В
1 2 k 1 2 n
частности, для первого игрока выполняется неравенство
k
ij i
au , 1 j n,
(3.1)
где – цена игры.
i1
В дальнейшем будем считать, что цена игры положительное чис- ло. Этого всегда можно добиться, так как, если добавить ко всем эле- ментам матрицы A одно и то же число, то это не приведет к измене- нию оптимальных стратегий, а только лишь увеличит на это число це-
ну игры. Разделим обе части (3.1) на :
k u
aij i 1,
1 j n.
(3.2)
Введем замену
i1
-
u
yi
тогда (3.2) перепишется так:
k
i,
1 i k,
(3.3)
ij i
i
ay 1, y 0, 1 j n, 1 i k.
(3.4)
i1
Условие (3.2) перепишем в следующем виде:
k
y 1.
(3.5)
i
i1
Первый игрок стремится получить максимальный выигрыш, сле- довательно, его оптимальная стратегия заключается в минимизации
величины 1/. То есть определение его оптимальной стратегии сво- дится к нахождению минимального значения функции
k
при начальных условиях:
k
F y
i
i1
(3.6)
aijyi
i1
1,
yi 0,
1 j n,
1 i k.
(3.7)
Аналогично и для второго игрока
aij
v
j 1,
1 i k.
(3.8)


