Файл: прикладная математика учебное пособие московский автомобильнодорожный.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.02.2024
Просмотров: 219
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Задачи выпуклого программирования
Решение задачи нелинейного программирования в Excel
Задания к самостоятельной работе
К ЗАДАЧАМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задания для самостоятельного решения
КООПЕРАТИВНЫЕ ИГРЫ И ДРУГИЕ ЗАДАЧИ
Параметры сетей и методы их расчета
Матричный метод расчета сетевого графика
Табличный метод расчета сетевого графика
Таблица стандартного нормального распределения
Анализ и оптимизация сетевой модели
Управление производством работ по сетевым графикам
Проект СРМ и временной резерв стадий
Проект СРМ и временной резерв стадий
где 1 i k
и 1
j n, необходимо и достаточно для того, чтобы u, v
были оптимальными стратегиями с ценой игры, равной .
Если игрок применяет оптимальную смешанную стратегию, то его выигрыш не будет зависеть от того, с какими частотами будет приме-
нять другой игрок стратегии, вошедшие в его оптимальную стратегию. Очевидно, что этот выигрыш будет равен цене игры.
- Пример задачи теории игр, заданной матрицей 22
Пример 1. Найти решение игры, заданной матрицей
8 2
A 1 5 .
Решение. 1. Проверим матрицу на наличие седловой точки:
max(minaij) 2, min(max aij) 5.
1i2
1 j2
1 j2 1i2
Так как 2 5, то решением игры будут смешанные стратегии, а
цена игры 2 5.
-
Пусть
u (u,u )
-
оптимальная стратегия первого игрока, то-
1 2
1 2
гда при 1-й стратегии второго игрока получаем, что
u 8u ,
а при
применении им 2-й стратегии
1 ... 9 10 11 12 13 14 15 16 ... 42
5u 2u .
Добавим еще одно усло-
1 2
1 2
вие u u 1 и получим систему уравнений:
1
2
u 8u ,
5u1 2u2 ,
u u 1.
1 2
-
Решение полученной системы:
u 0,6,
1
-
Пусть
v (v,v )
u 0,4,
2
3,8.
-
оптимальная стратегия второго игрока, то-
1 2
1 2
гда при 1-й стратегии первого игрока получается, что
v 5v , а
при применении им 2-й стратегии
8v 2v .
Добавим еще одно ус-
1 2
1 2
ловие v v 1,
и получим систему уравнений:
1
2
v 5v ,
8v1 2v2 ,
v v 1.
1 2
Решение полученной системы:
v 0,3,
1
2
v 0,7,
3,8.
6. Итак, решением игры являются следующие смешанные страте-
гии u (0,6; 0,4) и v (0,3; 0,7) с ценой игры, равной 3,8.
Графическое решение. Рассмотрим геометрическую интерпре- тацию решения поставленной выше задачи (рис. 2.1).
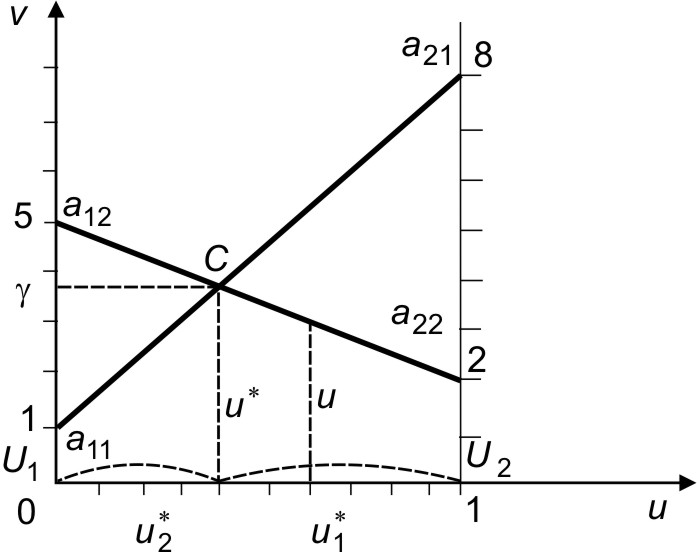
Рис.2.1.Графическоерешение
-
В плоскости uOvотложим вдоль оси Ouотрезок
[U1U2 ]
еди-
ничной длины. Тогда каждой его точке будет соответствовать какая-
либо смешанная стратегия
u (u1,u2 )
(см. рис. 2.1). В частности, чис-
той стратегии
U1 соответствует вектор
u (0,1),
а стратегии U2
вектор
1 ... 10 11 12 13 14 15 16 17 ... 42
u (1,0).
В точке U2
оси Ouпроведем к ней перпендикуляр. На оси
Ovотметим точки
a11 1 и
a12 5,
а на построенном перпендикуляре
точки
a21 8
и a22 2.
Соединим их пересекающимися в точке Сот-
резками, которые всегда пересекаются при отсутствии седловой точки.
-
В результате получаем ломаную линию
a11Ca22,
точки которой
определяют минимальный выигрыш первого игрока.
Следовательно, оптимальная стратегия
u (u,u )
соответству-
1 2
ет абсциссе точки С(наибольшее значение на ломаной), а ее ордина- та равна цене игры. Координаты точки Снаходятся геометрически из
подобия треугольников
a11Ca12
и a21Ca22.

u1
0,6,
0,4,
u2
a
u au 3,8.
11 1 21 2
-
Аналогично находится оптимальная стратегия
v (v,v )
вто-
1 2
рого игрока. В плоскости uOvотложим вдоль оси Ovотрезок
[V1V2 ]


