Файл: прикладная математика учебное пособие московский автомобильнодорожный.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.02.2024
Просмотров: 209
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Задачи выпуклого программирования
Решение задачи нелинейного программирования в Excel
Задания к самостоятельной работе
К ЗАДАЧАМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задания для самостоятельного решения
КООПЕРАТИВНЫЕ ИГРЫ И ДРУГИЕ ЗАДАЧИ
Параметры сетей и методы их расчета
Матричный метод расчета сетевого графика
Табличный метод расчета сетевого графика
Таблица стандартного нормального распределения
Анализ и оптимизация сетевой модели
Управление производством работ по сетевым графикам
Проект СРМ и временной резерв стадий
Проект СРМ и временной резерв стадий
единичной длины. В точке V2
оси Ovпроведем к ней перпендикуляр.
На оси Ouотметим точки
a11 1 и
a21 8,
а на построенном перпен-
дикуляре точки
a12 5,
a22 2
и соединим их пересекающимися в точ-
ке Сотрезками. В результате получим систему:
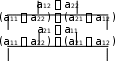
v1
0,3,
v2
a
v av 3,8.
0,7,
11 1 12 2
Замечание. Удобнее находить решения приведенных выше сис- тем, пользуясь правилом, чем-то схожим с правилом Крамера. То есть сначала вычисляем выражение знаменателя дробей, как модуль раз- ности сумм диагональных элементов матрицы A (аналогично вычис- лению определителя), а затем модуль разности дополнения к соот-
ветствующему столбцу или строке для u и vсоответственно.
- Примеры решения игр, заданных матрицами 2nи k2
Пример 2. Найти решение игры, заданной матрицей
7 4 9 5 3
A 3 5 1 4 6 .
Решение. 1. Проверим матрицу на наличие седловой точки:
max(minaij) 3, min(max aij) 6.
1i2
1 j5
1 j5 1i2
Так как 3 6, то решением игры будут смешанные стратегии, а
цена игры 3 6.
Графическое решение. 2. В плоскости uOvотложим вдоль оси
Ouотрезок
[U1U2 ]
единичной длины. Тогда каждой его точке будет со-
ответствовать какая-либо смешанная стратегия u (u1,u2 ), на рис. 2.2.
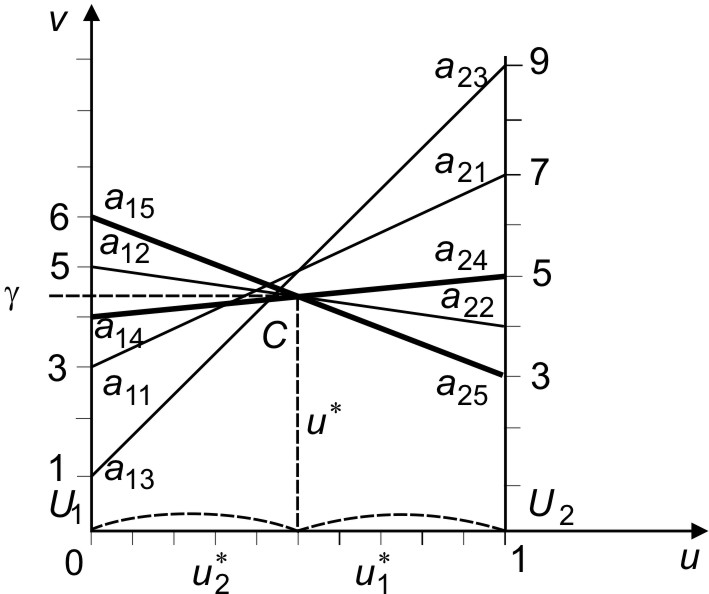
Рис.2.2.Графическоерешениеспятьювекторами
В точке U2
оси Ouпроведем к ней перпендикуляр. На оси Ov
отметим точки первой строки матрицы A, а, на построенном перпен-
дикуляре – точки второй ее строки и соединим их пересекающимися в точке Сотрезками.
-
В результате выбираем ломаную линию
a14Ca25
(самую ниж-
нюю из всех возрастающе-убывающих ломаных), точки которой опре- деляют минимальный выигрыш первого игрока. Следовательно, опти-
мальная стратегия
u (u,u )
соответствует абсциссе точки С(наи-
1 2
большее значение на ломаной), а ее ордината равна цене игры. Ко-
ординаты точки С находятся из подобия треугольников
a24Ca25
a14Ca15 и
5 3
A/ 4 6.
Таким образом, решение задачи свелось к решению матрицы A/
размерностью 2 2,
рицы A.
образованной 4-м и 5-м столбцами данной мат-
u
0,5,
1
u
0,5,
2
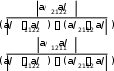 a/ u a/ u 4,5.
a/ u a/ u 4,5.
v
11 1 21 2
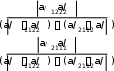 0,75,
0,75, 4
v
0,25,
5
a/ v a/ v 4,5.
11 4 12 5
-
Аналогично находится оптимальная стратегия
1 ... 11 12 13 14 15 16 17 18 ... 42
v (0,0,0,v,v )
4 5
второго игрока. В плоскости uOv отложим вдоль оси Ov отрезок
a
[V4V5 ]
единичной длины. В точке V5
оси Ovпроведем к ней перпенди-
a
11
a
4
и
куляр. На оси Ouотметим точки /
/ 5,
а, на построенном
a
21
12
6
и
перпендикуляре – точки /
/ 3.
Соединим их пересекающи-
22
мися в точке Cотрезками. В результате получим систему уравнений.
-
Итак, решением игры являются следующие смешанные страте-
гии u (0,5;0,6)
и v (0;0;0;0,75;0,25) с ценой игры, равной
4,5.
Пример 3. Найти решение игры, заданной матрицей
6 5
3 6
A .
2 7
1 8
Решение. 1. Проверим матрицу на наличие седловой точки:
max(minaij) 5, min(max aij) 6.
1i4
1 j2
1 j2 1i4
Так как 5 6, то решением игры будут смешанные стратегии, а
цена игры 5 6.
Графическое решение. 2. Находится оптимальная стратегия
1 2
v (v,v )
второго игрока. В плоскости uOvотложим вдоль оси Ov
отрезок
[V1V2 ]
единичной длины. В точке V2
оси Ovпроведем к ней
перпендикуляр. На оси Ouотметим точки первого столбца матрицы
A, а на построенном перпендикуляре – точки второго ее столбца и со-
единим их пересекающимися в точке Сотрезками (рис. 2.3).
-
В результате выбираем ломаную линию
a41Ca12
(самую верх-
нюю из всех убывающе-возрастающих), точки которой определяют максимальный проигрыш второго игрока. Следовательно, оптималь-
ная стратегия
v (v,v )
соответствует абсциссе точки С(наимень-
1 2
шее значение на ломаной), а ее ордината равна цене игры. Координа-
ты точки Снаходятся из подобия треугольников
a41Ca11 и
a42Ca12.
Та-
ким образом, решение задачи свелось к решению матрицы A/
раз-
мерностью 2 2, образованной 1-й и 4-й строками данной матрицы A.
1 8
A/ 6 5.
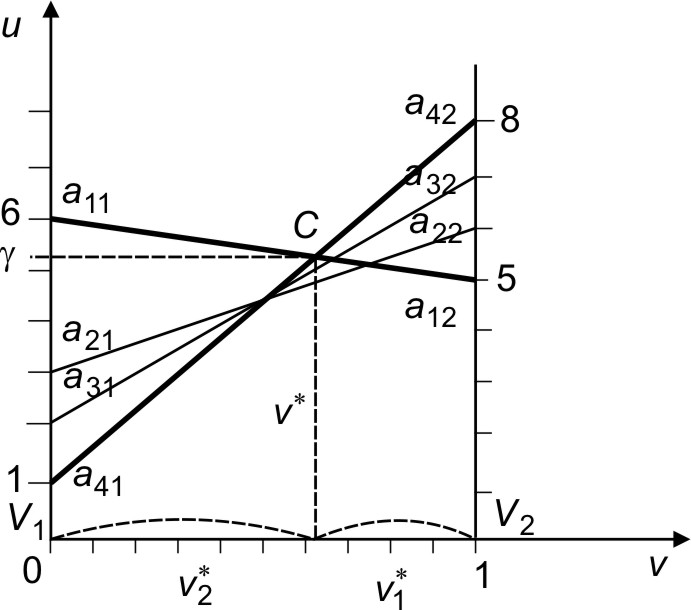
Рис.2.3.Графическоерешениесчетырьмявекторами
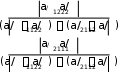 Ее решение:
Ее решение:

