Файл: прикладная математика учебное пособие московский автомобильнодорожный.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.02.2024
Просмотров: 234
Скачиваний: 0
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
СОДЕРЖАНИЕ
1. НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
Задачи выпуклого программирования
Решение задачи нелинейного программирования в Excel
Задания к самостоятельной работе
К ЗАДАЧАМ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задания для самостоятельного решения
КООПЕРАТИВНЫЕ ИГРЫ И ДРУГИЕ ЗАДАЧИ
Параметры сетей и методы их расчета
Матричный метод расчета сетевого графика
Табличный метод расчета сетевого графика
Таблица стандартного нормального распределения
Анализ и оптимизация сетевой модели
Управление производством работ по сетевым графикам
Проект СРМ и временной резерв стадий
Проект СРМ и временной резерв стадий
3 С3
3 С3
3 С3 10
6 6 6
Значения V({1,2,3}) 9,
V({1,2,4}) 19
и V({1,4,5}) 21 выбираются
из таблицы значений характеристической функции при
x 3, y
0,
x 2, y 1 и
x 1,
y 2,
а значения
V({2,3}) 6,
V({2,4}) 12 и
V({4,5}) 10 – при
x 2, y
0;
x 1,
y 1 и
x 0, y 2
соответственно.
-
Коалиция из четырех игроков: всего 10 вариантов:
S {1,2,3,4},{1,2,3,5},{1,2,3,6},{1,2,4,5},{1,2,4,6}, .
{1,2,5,6},{1,3,4,5},{1,3,4,6},{1,3,5,6},{1,4,5,6}
Из них равносильные:
S {{1, 4,5,6}}, S {{1,2,3,4},{1,2,3,5},{1,2,3,6}},
S {{1,2,4,5},{1,2,4,6},{1,2,5,6},{1,3, 4,5},{1,3, 4,6},{1,3,5,6}},
т.е. один штукатур и три маляра, три штукатура и один маляр, два шту- катура и два маляра. Следовательно, (4.1) слагаемое суммы равно




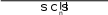
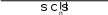 V({1,4,5,6}) V({4,5,6}) 3V({1,2,3,4}) V({2,3,4})
V({1,4,5,6}) V({4,5,6}) 3V({1,2,3,4}) V({2,3,4}) 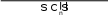 6 V({1,2, 4,5}) V({2,4,5}) 30 15 3 26 19 6 32 21 17 .
6 V({1,2, 4,5}) V({2,4,5}) 30 15 3 26 19 6 32 21 17 .




 4 С4
4 С44 С4
4 С4 10
6 6 6
-
Коалиция из пяти игроков: всего 5 вариантов:
S {{1,2,3, 4,5},{1,2,3, 4,6},{1,2,3,5,6},{1,2,4,5,6},{1,3, 4,5,6}}.
Из них равносильные:
S {{1,2,3, 4,5},{1,2,3, 4,6},{1,2,3,5,6}} и S {{1,2,4,5,6},{1,3, 4,5,6}},
т.е. три штукатура и два маляра, два штукатура и три маляра. Следо- вательно, пятое слагаемое (4.1) равно




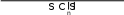
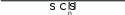 3 V({1,2,3, 4,5}) V({2,3, 4,5}) 2V({1,2, 4,5,6}) V({2,4,5,6})
3 V({1,2,3, 4,5}) V({2,3, 4,5}) 2V({1,2, 4,5,6}) V({2,4,5,6}) 3 43 32 2 45 30 21.



5 С5 5 С5 10
6 6
-
Коалиция из шести игроков: всего 1 вариант
S {{1,2,3,4,5,6}},
т.е. три штукатура и три маляра. Следовательно, шестое слагаемое
(4.1) равно
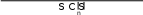 V({1,2,3, 4,5,6}) V({2,3,4,5,6}) 60 45 5 .
V({1,2,3, 4,5,6}) V({2,3,4,5,6}) 60 45 5 .

6

 6 С6 2
6 С6 2 Итак, для каждого штукатура получается:
(V)
(V)
(V) 1 9

13 17 21 5 9.




1 2 3

2 10 10 10 10 2
Аналогично рассматриваются все возможные варианты коалиций с четвертым игроком.
1. Коалиция из одного игрока:
S {{4}}
-
единственный вариант.
Следовательно, первое слагаемое (4.1) равно
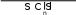
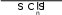 V(S) V(S\ {4}) V({4}) V() 5 0 5 .
V(S) V(S\ {4}) V({4}) V() 5 0 5 .

6



 1 С1 6
1 С1 6 Значение
V({4})
выбирается из таблицы значений характеристи-
ческой функции (см. табл. 4.1) при
x 0, y
1.
2. Коалиция из двух игроков: S {{1,4},{2,4},{3, 4},{4,5},{4,6}} –
всего 5 вариантов. Из них равносильные:
{{4,5},{4,6}} и {{1,4},{2,4},{3, 4}},
т.е. два маляра или один маляр и один штукатур. Следовательно, второе слагаемое (4.1) равно
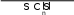
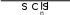 2V({4,5}) V({5}) 3 V({1, 4}) V({1}) 210 5 312 3 37 .
2V({4,5}) V({5}) 3 V({1, 4}) V({1}) 210 5 312 3 37 .





 2 С2 2 С2 30
2 С2 2 С2 30Значения V({4,5}) 10
и V({1,4}) 12
6 6
выбираются из таблицы зна-
чений характеристической функции (см. табл. 4.1) при x 0, y 2 и
x 1,
y 1,
а значения
V({1}) 3
и V({5}) 5
– при
x 1,
y 0 и
x 0, y 1 соответственно.
-
Коалиция из трех игроков: всего 10 вариантов:
S {1,2,4}, {1,3,4}, {2,3,4}, {1,4,5}, {1,4,6}, {2,4,5}, .
{2,4,6}, {3,4,5}, {3,4,6}, {4,5,6}
Из них равносильные:
S { {1,4,5}, {1,4,6}, {2,4,5},{2,4,6}, {3,4,5}, {3,4,6}}.
S { {4,5,6}}, S { {1,2,4},{1,3,4},{2,3,4}},
т.е. один штукатур и два маляра, три маляра, два штукатура и один маляр. Следовательно, третье слагаемое (4.1) равно






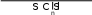
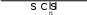
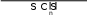 V({4,5,6}) V({5,6}) 6 V({1, 4,5}) V({1,5}) 3 V({1,2,4}) V({1,2})
V({4,5,6}) V({5,6}) 6 V({1, 4,5}) V({1,5}) 3 V({1,2,4}) V({1,2}) 15 10 6 21 12 3 19 6 49 .






