ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 20.10.2024
Просмотров: 306
Скачиваний: 0
СОДЕРЖАНИЕ
Часть I. Способы передачи сообщений
1.1 Спектры периодических сигналов
1.2. Спектры непериодических сигналов
1.3. Сигналы электросвязи и их спектры
2.1. Принципы передачи сигналов электросвязи
3.1. Понятие о цифровых сигналах
3.2. Дискретизация аналоговых сигналов
3.3. Квантование и кодирование
3.4. Восстановление аналоговых сигналов
Глава 4. Принципы многоканальной передачи
4.1. Одновременная передача сообщений
4.2. Частотное разделение каналов
4.3. Временное разделение каналов
Глава 5. Цифровые системы передачи
5.1. Формирование группового сигнала
6.3. Регенерация цифровых сигналов
5.4. Помехоустойчивое кодирование
6.1. Плезиохронная цифровая иерархия
6.2. Синхронная цифровая иерархия
7.3. Волоконно-оптические кабельные линии
8.1. Предпосылки создания транспортных сетей
8.2. Системы передачи для транспортной сети
Vc низшего порядка (Low order vc, lovc)
Vc высшего порядка (High order vc, hovc)
8.3. Модели транспортных сетей
8.4. Элементы транспортной сети
8.5. Архитектура транспортных сетей
Часть II. Службы электросвязи. Телефонные службы и службы документальной электросвязи
Глава 9. Основные понятия и определения
9.1. Информация, сообщения, сигналы
9.2. Системы и сети электросвязи
9.3. Эталонная модель взаимосвязи открытых систем
9.4. Методы коммутации в сетях электросвязи
9.5 Методы маршрутизации в сетях электросвязи
Т а б л и ц а 9.2. Устройства, реализующие функции маршрутизации
10.1. Услуги, предоставляемые общегосударственной системой автоматизированной телефонной связи
10.3. Расчет коммутационного узла с коммутацией каналов 10.3.1. Модель коммутационного узла
10.3.1 Модель коммутационного узла
10.3.2. Структура коммутационных полей станций и узлов
10.3.3. Элементы теории телетрафика
11.2. Направления развития телеграфной связи
Глава 12. Службы пд. Защита от ошибок и преобразование сигналов
12.2. Сигналы и виды модуляции, используемые в современных модемах
13.1. Компьютеры — архитектура и возможности
13.2. Принципы построения компьютерных сетей
13.3. Международные стандарты на аппаратные и программные средства компьютерных сетей
13.4. Сетевые операционные системы
13.5. Локальные компьютерные сети
13.6. Глобальные компьютерные сети
13.7. Телефонная связь по компьютерным сетям
14.1. Основы факсимильной связи
14.2. Организация факсимильной связи
Глава 15. Другие службы документальной электросвязи
Глава 16. Единая система документальной электросвязи
16.1. Интеграция услуг документальной электросвязи [1]
16.2. Назначение и основные принципы построения служб обработки сообщений [2]
16.3. Многофункциональные терминалы
Глава 17. Обеспечение информационной безопасности в телекоммуникационных системах
17.2. Правовые и организационные аспекты информационной безопасности
17.3. Технические аспекты информационной безопасности
Часть III. Интеграция сетей и служб электросвязи
Глава 18. Узкополосные цифровые сети интегрального обслуживания (у-цсио)
18.1. Пути перехода к узкополосной цифровой сети интегрального обслуживания
18.2. Службы и услуги узкополосной цсио
18.3. Система управления у-цсио
Глава 19. Широкополосные и интеллектуальные сети
19.1. Условия и этапы перехода к широкополосной сети интегрального обслуживания (ш-цсио)
19.3. Способы коммутации в ш-цсио
19.4. Построение коммутационных полей станций ш-цсио
19.5. Причины и условия перехода к интеллектуальной сети (ис)
Глава 20. Система межстанционной сигнализации по общему каналу в цсио
20.1. Понятие об общем канале сигнализации
20.2. Протоколы системы сигнализации № 7 itu-t
20.3. Способы защиты от ошибок в окс № 7
20.5. Способы построения сигнальной сети
Глава 21. Широкополосные сети и оборудование компании «Huawei Technologies Co, Ltd»
21.1. Оптическая сеть абонентского доступа с интеграцией услуг honet
21.2. Построение транспортных сетей на базе оборудования компании «Huawei Technologies Co., Ltd»
21.3. Цифровая коммутационная система с программным управлением с&с08
21.4. Высокоскоростной коммутирующий маршрутизатор Radium 8750
Часть IV. Современные методы управления в телекоммуникациях
22.1. Многоуровневое представление задач управления телекоммуникациями
22.2. Функциональные группы задач управления
Глава 23. Интегрированные информационные системы управления предприятиями электросвязи
23.1. Понятия и определения в области информационных систем управления предприятием
Глава 24. Управление услугами. Качество предоставляемых услуг
24.1. Система качества услуг электросвязи
24.2. Базовые составляющие обеспечения качества услуги
24.3. Оценка качества услуг связи с точки зрения пользователя и оператора связи
Глава 25. Управление услугами.
25.3. Централизованный способ построения системы расчетов
25.4. Интеграция аср с системами управления tmn
25.5. Основные технические требования для аср
25.6. Обзор автоматизированных систем расчетов
Глава 26. Управление сетями и сетевыми элементами
26.1. Архитектура систем управления сетями и сетевыми элементами
26.2. Системы управления первичными и вторичными сетями
26.3. Принципы построения системы управления
Глава 27. Решения компании strom telecom в области tmn (Foris oss)
27.1. Общая характеристика семейства продуктов Foris oss
27.2. Автоматизация расчетов. Подсистема TelBill
27.3. Многофункциональные подсистемы сбора данных и взаимодействия с атс
27.4. Подсистема сбора данных и их биллинговой предобработки TelCharge
27.5. Подсистемы TelRes, TelTe, TelRc
27.6. Система «Электронный замок»
27.7. Подсистема поддержки клиентов tccs (Foris Customer Care Systems)
Алгоритм формирования проверочных элементов а5, а6, а7 может быть задан матрицей, называемой проверочной. Эта матрица содержит r строк и n столбцов. Применительно к сформированному нами коду (7,4) она имеет вид:

Единицы, расположенные на местах, соответствующих информационным элементам матрицы Н(7,4), указывают на то, какие информационные элементы должны участвовать в формировании проверочного элемента. Единица на месте, соответствующем проверочному элементу, указывает, какой проверочный элемент получается при суммировании по модулю два информационных элементов. Так, из первой строки следует равенство
![]()
Процедура обнаружения ошибок основана на использовании проверок (12.4)-(12.6). Очевидно, что проверочные элементы, сформированные из принятых информационных, при отсутствии ошибок должны совпадать с принятыми проверочными.
Пример
12.3. Переданная
кодовая комбинация имеет вид 1000111 (первая
строка матрицы (12.3)). В результате действия
помех на приемном конце имеем
![]() .
Произведем проверки (12.4)-(12.6):
.
Произведем проверки (12.4)-(12.6):
![]() ,
(12.7)
,
(12.7)
![]() (12.8)
(12.8)
![]() (12.9)
(12.9)
В то
же время
![]() ,
т.е.
,
т.е.
![]() ,
что
говорит о наличии ошибок в принятой
кодовой комбинации. При отсутствии в
принятой кодовой комбинации ошибок
,
что
говорит о наличии ошибок в принятой
кодовой комбинации. При отсутствии в
принятой кодовой комбинации ошибок
![]() ,
,
![]() ,
,
![]()
Комбинация b3b2b1 называется синдромом (проверочным вектором). Равенство нулю всех элементов синдрома указывает на отсутствие ошибок или на то, что кодовая комбинация принята с ошибками, которые превратили ее в другую разрешенную. Последнее событие имеет существенно меньшую вероятность, чем первое.
Вид ненулевого синдрома определяется характером ошибок в кодовой комбинации. В нашем случае вид синдрома зависит от местоположения одиночной ошибки. В табл. 12.2 отражено соответствие между местоположением одиночной ошибки для кода, заданного матрицей (12.3), и видом синдрома.
Таблица 12.2. Местоположение ошибки и вид синдрома
|
Номер элемента, в котором произошла ошибка |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Вид синдрома |
111 |
101 |
110 |
011 |
001 |
010 |
100 |
Таким образом, зная вид синдрома, можно определить место, где произошла ошибка, и исправить принятый элемент на противоположный.
Пример 12.4. Передавалась кодовая комбинация 1000111. Принята кодовая комбинация 0000111. Синдром имеет вид 111. В соответствии с табл. 12.2 исказился первый элемент (а1). Изменим первый элемент на противоположный:
![]()
![]()
Полученная в результате исправления ошибки кодовая комбинация совпадает с переданной.
Рассмотренный код (7,4) гарантированно обнаруживает двухкратные ошибки, а исправляет только однократные ошибки.
Циклические коды. В теории циклических кодов кодовые комбинации обычно представляются в виде полинома. Так, п-элементная кодовая комбинация записывается в виде
A(x) = an-1xn-1 + an-2xn-2 + … + a1x + a0,
где ai = {0,1}, причем аi = 0 соответствуют нулевым элементам комбинации, а аi = 1 - ненулевым. Например, комбинациям 1101 и 1010 соответствуют многочлены A1(х) = х3 + х2 +1 и А2(х) = х3 + х.
При формировании комбинаций циклического кода часто используют операции сложения многочленов и деления одного многочлена на другой. Так,
A1(х) + A2(х) = (х3 + х2 +1) + (х3 + х) = х2 + х +1,
поскольку
х3
+ х3
= х3(1![]() 1)
= 0.
1)
= 0.
Рассмотрим операцию деления на следующем примере:
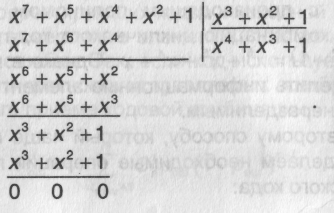
![]() Таким
образом, зная вид синдрома, можно
определить место, где произошла ошибка,
и исправить принятый элемент на
противоположный.
Таким
образом, зная вид синдрома, можно
определить место, где произошла ошибка,
и исправить принятый элемент на
противоположный.
Деление выполняется, как обычно, только вычитание заменяется суммированием по модулю два.
Разрешенные комбинации циклического кода обладают двумя очень важными отличительными признаками: циклический сдвиг разрешенной комбинации тоже приводит к разрешенной кодовой комбинации. Все разрешенные кодовые комбинации делятся без остатка на полином Р(х), называемый образующим. Эти свойства используются при построении кодов, кодирующих и декодирующих устройств, а также при обнаружении и исправлении ошибок.
Найдем алгоритмы построения циклического кода, удовлетворяющего перечисленным выше условиям. Задан полином Р(х) = ar-1xr + ar-2xr-1 + ... + 1, определяющий корректирующую способность кода, и задан исходный простой код, который требуется преобразовать в корректирующий циклический.
Обозначим многочлен, соответствующий комбинации простого кода, Q(x). Возьмем произведение Q(х)xr разделим его на Р(х). В результате получим многочлен G(x) и остаток R(x)/P(x):
![]() (12.10)
(12.10)
Умножим левую и правую части на Р(х), тогда (12.10) перепишется в виде
Q(x)xr = G(x)P(x) + R(x) (12.11)
Перепишем равенство (12.11) в виде
G(x)P(x) = Q(x)xr + R(x) (12.12)
Левая часть (12.12) делится без остатка на Р(х), значит, без остатка делится и правая часть. Из (12.12) вытекают два способа формирования комбинаций циклического кода: путем умножения многочлена G(x) на Р(х) и путем деления Q(х)xr на Р(х) и приписывания к Q(x)xr остатка от деления R(х).
Пример 12.5. Задан полином G(x) = x3 + x, соответствующий комбинации простого кода. Сформировать комбинацию циклического кода (7,4) с производящим полиномом Р(х) = х3 + х2 + 1. Можно получить комбинацию циклического кода в виде G(x)P(x) = = (х3 + х)(х3 + х2 +1) = х6 + х5 + х4 + х. Однако в полученной комбинации нельзя отделить информационные элементы от проверочных, и код получается неразделимым.
Перейдем ко второму способу, который чаще всего применяется на практике. Проделаем необходимые операции по получению комбинации циклического кода:
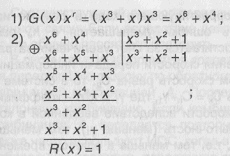
3) (х6 + х4+1) - комбинация циклического кода, полученная методом деления на производящий полином. Она может быть переписана в виде 1010001. Первые четыре элемента - информационные, последние три - проверочные, т.е. полученный код - разделимый.
Для обнаружения ошибок в принятой кодовой комбинации достаточно поделить ее на производящий полином. Если принятая комбинация разрешенная, то остаток от деления будет нулевым. Ненулевой остаток свидетельствует о том, что принятая комбинация содержит ошибки. По виду остатка (синдрома) можно в некоторых случаях также сделать вывод о характере ошибки и исправить ее.
Циклические коды достаточно просты в реализации, обладают высокой корректирующей способностью (способностью исправлять и обнаруживать ошибки) и поэтому рекомендованы МСЭ-Т для применения в аппаратуре ПД. Согласно рекомендации V.41 в системах ПД с ОС рекомендуется применять код с производящим полиномом Р(х) = х16 + х12 + х5+1.
Эффективность применения корректирующих кодов. Полезный эффект от применения корректирующих кодов заключается в повышении верности. Вероятность неправильного приема кодовой комбинации простого кода определяется как вероятность появления в кодовой комбинации хотя бы одной ошибки, т.е.
![]()
где PОШ - вероятность неправильного приема единичного элемента; k - число элементов в комбинации простого кода. При применении систематических корректирующих кодов к исходной кодовой комбинации добавляются проверочные элементы, позволяющие исправлять или обнаруживать ошибки. Так, если код используется в режиме исправления ошибок и кратность исправляемых ошибок tи.ош, то вероятность неправильного приема кодовой комбинации
![]()
В
результате применения корректирующего
кода в режиме ис-правления ошибок
вероятность ошибки уменьшается в Ки
раз:
![]() .
Однако это достигается за счет увеличения
затрат на реализацию системы и снижения
скорости передачи информации. Если в
системе с простым кодом скорость равна
Сп,
то в системе с корректирующим кодом
скорость
.
Однако это достигается за счет увеличения
затрат на реализацию системы и снижения
скорости передачи информации. Если в
системе с простым кодом скорость равна
Сп,
то в системе с корректирующим кодом
скорость
![]() -
коэффициент,
характеризующий потери скорости
вследствие введенной в код избыточности.
Чем больше избыточность (меньше
-
коэффициент,
характеризующий потери скорости
вследствие введенной в код избыточности.
Чем больше избыточность (меньше
![]() ).
тем
меньше скорость передачи информации,
т.е. тем меньше в единицу времени
передается полезной информации.
).
тем
меньше скорость передачи информации,
т.е. тем меньше в единицу времени
передается полезной информации.
Качество реальных каналов во времени меняется, и если заданы требования на верность передачи, то необходимо ввести такую избы-точность, которая обеспечивала бы заданную верность даже при са-мом плохом качестве канала. Напрашивается мысль о целесообраз-ности изменения избыточности, вводимой в кодовую комбинацию, по мере изменения характеристик канала связи. Системы, в которых меняется избыточность с изменением качества канала, относятся к чис-лу адаптивных. Одним из типов адаптивных систем являются систе-мы с обратной связью. В этих системах между приемником и пере-датчиком помимо основного (прямого) канала имеется вспомогательный (обратный).

